Manual Fundamentos del Aprendizaje Automático Conceptos clave, algoritmos y ejemplos de código en Python

Manual de Fundamentos de Aprendizaje Automático Conceptos Clave, Algoritmos y Ejemplos de Código en Python

Si estás planeando convertirte en Ingeniero de Aprendizaje Automático, Científico de Datos, o si quieres refrescar tu memoria antes de tus entrevistas, este manual es para ti.

En él, cubriremos los algoritmos clave de Aprendizaje Automático que deberás conocer como Científico de Datos, Ingeniero de Aprendizaje Automático, Investigador de Aprendizaje Automático e Ingeniero de IA.

A lo largo de este manual, incluiré ejemplos para cada algoritmo de Aprendizaje Automático con su código en Python para ayudarte a comprender lo que estás aprendiendo.

Ya seas un principiante o tengas algo de experiencia en Aprendizaje Automático o IA, esta guía está diseñada para ayudarte a comprender los fundamentos de los algoritmos de Aprendizaje Automático a un alto nivel.

Como practicante experimentado de aprendizaje automático, estoy emocionado de compartir mi conocimiento y perspectivas contigo.

Lo que aprenderás

1. Capítulo 1: ¿Qué es el Aprendizaje Automático?
2. Capítulo 2: Los algoritmos de Aprendizaje Automático más populares

• 2.1 Regresión Lineal y Mínimos Cuadrados Ordinarios (OLS)
• 2.2 Regresión Logística y MLE
• 2.3 Análisis Discriminante Lineal (LDA)
• 2.4 Regresión Logística vs LDA
• 2.5 Naïve Bayes
• 2.6 Naïve Bayes vs Regresión Logística
• 2.7 Árboles de Decisión
• 2.8 Bagging
• 2.9 Bosques Aleatorios
• 2.10 Técnicas de refuerzo o ensamblaje (AdaBoost, GBM, XGBoost)

3.  Capítulo 3: Selección de Características

• 3.1 Selección de Subconjuntos
• 3.2 Regularización (Ridge y Lasso)
• 3.3 Reducción de Dimensionalidad (PCA)

4.  Capítulo 4: Técnica de remuestreo

• 4.1 Validación Cruzada: (Conjunto de Validación, LOOCV, CV-k)
• 4.2 k óptimo en CV-k
• 4.5 Bootstrap

5.  Capítulo 5: Técnicas de Optimización

• 5.1 Técnicas de Optimización: Descenso de Gradiente en Lote (GD)
• 5.2 Técnicas de Optimización: Descenso de Gradiente Estocástico (SGD)
• 5.3 Técnicas de Optimización: SGD con Momentum
• 5.4 Técnicas de Optimización: Adam Optimizer

6. Conclusiones

• 6.1 Puntos clave y qué viene a continuación
• 6.2 Sobre el Autor – ¡Eso soy yo!
• 6.3 ¿Cómo puedes profundizar más?
• 6.4 Conéctate conmigo

Prerrequisitos

Para aprovechar al máximo este manual, será útil que estés familiarizado/a con algunos conceptos básicos de ML:

Terminología básica:

• Datos de Entrenamiento y Datos de Prueba: Conjuntos de datos utilizados para entrenar y evaluar modelos.
• Características: Variables que ayudan en las predicciones, también llamadas variables independientes
• Variable Objetivo: El resultado predicho, también llamado variable dependiente o variable de respuesta

Problema de Sobreajuste en el Aprendizaje Automático

Comprender el sobreajuste, cómo está relacionado con el equilibrio sesgo-varianza y cómo puedes solucionarlo es muy importante. También examinaremos las técnicas de regularización en detalle en esta guía. Para una comprensión detallada, consulta:

Equilibrio Sesgo-Varianza, Sobreajuste y Regularización en el Aprendizaje AutomáticoEl sobreajuste es un problema importante que forma parte esencial de la lista de verificación de modelos de cada científico de datos e ingeniero de aprendizaje automático. Por lo tanto, si estás utilizando una estadística, econometría o…Tatev Karen AslanyanTowards Data Science

Lecturas Fundamentales para Principiantes

Si no tienes conocimientos estadísticos previos y quieres aprender o refrescar tu entendimiento de conceptos estadísticos esenciales, te recomendaría este artículo: Conceptos Estadísticos Fundamentales para la Ciencia de Datos

Para una guía exhaustiva sobre cómo iniciar una carrera en Ciencia de Datos e Inteligencia Artificial, y obtener información sobre cómo asegurar un empleo en Ciencia de Datos, puedes sumergirte en mi manual anterior: Lanzando tu Carrera en Ciencia de Datos e Inteligencia Artificial

Herramientas/Lenguajes para usar en Aprendizaje Automático

Como Investigador en Aprendizaje Automático o Ingeniero en Aprendizaje Automático, hay muchas herramientas técnicas y lenguajes de programación que podrías usar en tu trabajo diario. Pero para hoy y para este manual, utilizaremos el lenguaje de programación y las herramientas:

1. Conceptos Básicos de Python: Variables, tipos de datos, estructuras y mecanismos de control.
2. Bibliotecas Esenciales: numpy, pandas, matplotlib,  scikit-learn, xgboost
3. Entorno: Familiaridad con Jupyter Notebooks o PyCharm como IDE.

Embarcarse en este viaje de Aprendizaje Automático con una base sólida asegura una experiencia más profunda e iluminadora.

¿Listos para empezar?

Capítulo 1: ¿Qué es el Aprendizaje Automático?

El Aprendizaje Automático (AA), una rama de la inteligencia artificial (IA), se refiere a la capacidad de una computadora de aprender autónomamente de los patrones de datos y tomar decisiones sin programación explícita. Las máquinas utilizan algoritmos estadísticos para mejorar la toma de decisiones del sistema y el rendimiento de tareas.

En su esencia, el AA es un método en el cual las computadoras mejoran en tareas mediante el aprendizaje de datos. Imagínalo como enseñarle a una computadora a tomar decisiones proporcionándole ejemplos, de manera similar a cómo enseñarías a un niño a reconocer animales mostrándole imágenes.

Por ejemplo, al analizar patrones de compra, los algoritmos de AA pueden ayudar a las plataformas de compras en línea a recomendar productos (como cuando Amazon sugiere artículos que podrías gustarte).

O considera las plataformas de correo electrónico que aprenden a identificar el spam reconociendo patrones en los correos no deseados. Mediante técnicas de AA, las computadoras mejoran silenciosamente nuestras experiencias digitales diarias, haciendo que las recomendaciones sean más precisas y protegiendo nuestras bandejas de entrada.

En este viaje, descubrirás el fascinante mundo del AA, donde la tecnología aprende y crece a partir de la información que encuentra. Pero antes de hacerlo, echemos un vistazo a algunos conceptos básicos en Aprendizaje Automático que debes conocer para entender cualquier tipo de modelo de Aprendizaje Automático.

Tipos de Aprendizaje en Aprendizaje Automático:

Existen tres formas principales en las que los modelos pueden aprender:

• Aprendizaje Supervisado: Los modelos hacen predicciones a partir de datos etiquetados (tienes características y etiquetas, X e Y)
• Aprendizaje No Supervisado: Los modelos identifican patrones de manera autónoma, donde no tienes datos etiquetados (solo tienes características sin variable de respuesta, solo X)
• Aprendizaje por Refuerzo: Los algoritmos aprenden a través de retroalimentación de acciones.

Métricas de Evaluación de Modelos:

En Aprendizaje Automático, cada vez que entrenas un modelo siempre debes evaluarlo. Y querrás utilizar el tipo más común de métricas de evaluación dependiendo de la naturaleza de tu problema.

A continuación, se muestran las métricas de evaluación más comunes para cada tipo de modelo de AA:

1. Métricas de Regresión:

• MAE, MSE, RMSE: Miden las diferencias entre los valores predichos y los reales.
• R-Cuadrado: Indica la varianza explicada por el modelo.

2. Métricas de Clasificación:

• Precisión, Exhaustividad, Puntuación F1: Evalúan la calidad de las predicciones.
• Curva ROC, AUC: Evalúan el poder discriminatorio del modelo.
• Matriz de Confusión: Compara las clasificaciones reales y las predichas.

3. Métricas de Agrupamiento:

• Puntuación de Silueta: Evalúa la similitud de objetos dentro de grupos.
• Índice de Davies-Bouldin: Evalúa la separación de los grupos.

Capítulo 2: Los Algoritmos de Aprendizaje Automático más Populares

En este capítulo, simplificaremos la complejidad de los algoritmos esenciales de Aprendizaje Automático (AA). Esto será un recurso valioso para roles que van desde Científicos de Datos e Ingenieros en Aprendizaje Automático hasta Investigadores en IA.

Comenzaremos con los conceptos básicos en el 2.1 con Regresión Lineal y Mínimos Cuadrados Ordinarios (OLS), luego pasaremos al 2.2 que explora Regresión Logística y Estimación de Máxima Verosimilitud (MLE).

La sección 2.3 explora el Análisis Discriminante Lineal (LDA), que se contrasta con la Regresión Logística en el 2.4. Entramos en Naïve Bayes en el 2.5, ofreciendo un análisis comparativo con la Regresión Logística en el 2.6.

En el 2.7, repasamos los Árboles de Decisión, para luego explorar métodos de conjunto: Bagging en el 2.8 y Bosque Aleatorio en el 2.9. Diversas y populares técnicas de Boosting se despliegan en los siguientes segmentos, discutiendo AdaBoost en el 2.10, Modelo de Boosting de Gradientes (GBM) en el 2.11 y concluyendo con Extreme Gradient Boosting (XGBoost) en el 2.12.

Todos los algoritmos que discutiremos aquí son fundamentales y populares en el campo, y todo Científico de Datos, Ingeniero de Aprendizaje Automático e Investigador de Inteligencia Artificial debe conocerlos al menos a este nivel alto.

Tenga en cuenta que aquí no profundizaremos en las técnicas de aprendizaje no supervisado ni entraremos en detalles granulares de cada algoritmo.

2.1 Regresión Lineal

Cuando la relación entre dos variables es lineal, se puede utilizar el método estadístico de Regresión Lineal. Puede ayudarte a modelar el impacto de un cambio unitario en una variable, la variable independiente, en los valores de otra variable, la variable dependiente.

Las variables dependientes se suelen denominar variables de respuesta o variables explicadas, mientras que las variables independientes se suelen denominar variables regresoras o variables explicativas.

Cuando el modelo de Regresión Lineal se basa en una sola variable independiente, se llama Regresión Lineal Simple. Pero cuando el modelo se basa en múltiples variables independientes, se llama Regresión Lineal Múltiple.

La Regresión Lineal Simple se puede describir mediante la siguiente expresión:

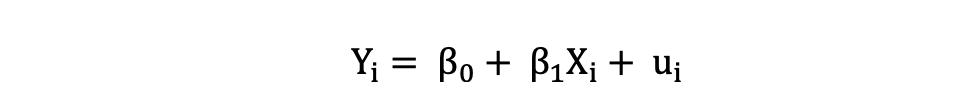
donde Y es la variable dependiente, X es la variable independiente que forma parte de los datos, β0 es la intersección que es desconocida y constante, y β1 es el coeficiente de pendiente o un parámetro correspondiente a la variable X que también es desconocida y constante. Por último, u es el término de error que el modelo comete al estimar los valores de Y.

La idea principal detrás de la regresión lineal es encontrar la línea recta que mejor se ajusta, la línea de regresión, a través de un conjunto de datos emparejados (X, Y). Un ejemplo de la aplicación de Regresión Lineal es modelar el impacto de la longitud de las aletas en la masa corporal de los pingüinos, que se visualiza a continuación:

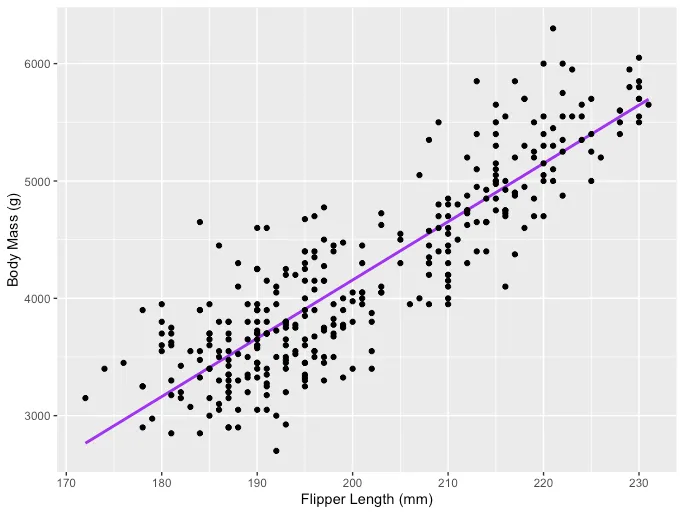
La Regresión Lineal Múltiple con tres variables independientes se puede describir mediante la siguiente expresión:

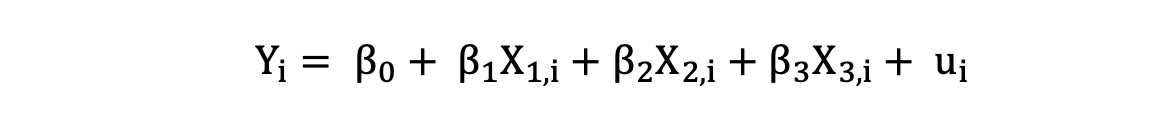
donde Y es la variable dependiente, X es la variable independiente que forma parte de los datos, β0 es la intersección que es desconocida y constante, y β1, β2, β3 son los coeficientes de pendiente o parámetros correspondientes a las variables X1, X2, X3 que también son desconocidos y constantes. Por último, u es el término de error que el modelo comete al estimar los valores de Y.

2.1.1 Mínimos Cuadrados Ordinarios

Los mínimos cuadrados ordinarios (OLS) es un método para estimar los parámetros desconocidos como β0 y β1 en un modelo de regresión lineal. El modelo se basa en el principio de los mínimos cuadrados que minimiza la suma de los cuadrados de las diferencias entre la variable dependiente observada y sus valores predichos por la función lineal de la variable independiente, a menudo llamados valores ajustados.

La diferencia entre los valores reales y los valores predichos de la variable dependiente Y se denomina residual. Lo que hace el MCO es minimizar la suma de los residuos cuadrados. Este problema de optimización da como resultado las siguientes estimaciones del MCO para los parámetros desconocidos β0 y β1, que también se conocen como estimaciones de coeficientes.

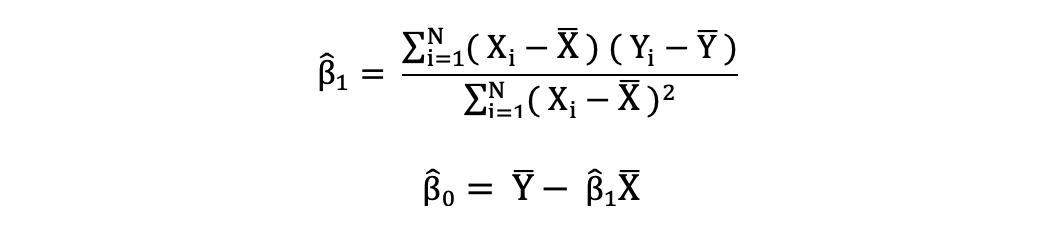
Una vez que se estiman estos parámetros del modelo de Regresión Lineal Simple, los valores ajustados de la variable de respuesta se pueden calcular de la siguiente manera:

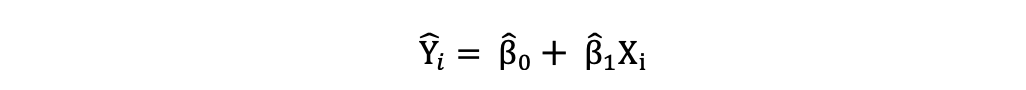
Error estándar

Los residuos o los términos de error estimados se pueden determinar de la siguiente manera:

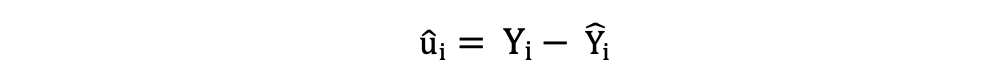
Es importante tener en cuenta la diferencia entre los términos de error y los residuos. Los términos de error nunca se observan, mientras que los residuos se calculan a partir de los datos. El MCO estima los términos de error para cada observación pero no el término de error real. Por lo tanto, la verdadera varianza del error sigue siendo desconocida.

Además, estas estimaciones están sujetas a incertidumbre de muestreo. Esto significa que nunca podremos determinar la estimación exacta, el valor real, de estos parámetros a partir de datos de muestra en una aplicación empírica. Pero podemos estimarlo calculando la varianza residual de la muestra.

2.1.2 Supuestos del MCO

El método de estimación del MCO hace los siguientes supuestos que deben cumplirse para obtener resultados de predicción confiables:

• Asunción (A)1: la asunción de Linealidad afirma que el modelo es lineal en los parámetros.
• A2: la asunción de Muestra aleatoria afirma que todas las observaciones de la muestra se seleccionan al azar.
• A3: la asunción de Exogeneidad afirma que las variables independientes no están correlacionadas con los términos de error.
• A4: la asunción de Homocedasticidad afirma que la varianza de todos los términos de error es constante.
• A5: la asunción de No Multicolinealidad Perfecta afirma que ninguna de las variables independientes es constante y no hay relaciones lineales exactas entre las variables independientes.

Tenga en cuenta que la descripción anterior para la Regresión Lineal es de mi artículo titulado Guía completa de Regresión Lineal.

Para obtener un artículo detallado sobre Regresión Lineal, consulte esta publicación:

Guía completa de Regresión LinealGuía completa de la técnica de Machine Learning más popular y simple, la Regresión Lineal., incluida su implementación en Python. Lo primero que puedes leer en cualquier libro de estadísticas es que la correlación no implica causalidad. Sin embargo, es lo primero que muchos estudiantes olvidan una vez que ven sus …Tatev Karen AslanyanHacia la IA

2.1.3 Regresión Lineal en Python

Imagina que tienes un amigo, Alex, que colecciona sellos. Cada mes, Alex compra una cierta cantidad de sellos, y notas que la cantidad que Alex gasta parece depender del número de sellos comprados.

Ahora, quieres crear una pequeña herramienta que pueda predecir cuánto gastará Alex el próximo mes en función del número de sellos comprados. Aquí es donde entra en juego la Regresión Lineal.

En términos técnicos, estamos tratando de predecir la variable dependiente (cantidad gastada) en función de la variable independiente (número de sellos comprados).

A continuación se muestra un código Python simple que utiliza scikit-learn para realizar una Regresión Lineal en un conjunto de datos creado.

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression# Datos de ejemplostamps_bought = np.array([1, 3, 5, 7, 9]).reshape((-1, 1))  # Reshape para convertirlo en una matriz 2Damount_spent = np.array([2, 6, 8, 12, 18])# Creación del modelo de Regresión Linealmodel = LinearRegression()# Entrenamiento del modelomodel.fit(stamps_bought, amount_spent)# Prediccionesnext_month_stamps = 10predicted_spend = model.predict([[next_month_stamps]])# Gráficoplt.scatter(stamps_bought, amount_spent, color='blue')plt.plot(stamps_bought, model.predict(stamps_bought), color='red')plt.title('Sellos Comprados vs Cantidad Gastada')plt.xlabel('Sellos Comprados')plt.ylabel('Cantidad Gastada ($)')plt.grid(True)plt.show()# Mostrar la predicciónprint(f"Si Alex compra {next_month_stamps} sellos el próximo mes, es probable que gaste ${predicted_spend[0]:.2f}.")

• Datos de ejemplo: stamps_bought representa el número de sellos que Alex compró cada mes y amount_spent representa el dinero gastado correspondiente.
• Creación y entrenamiento del modelo: Utilizando LinearRegression() de scikit-learn para crear y entrenar nuestro modelo usando .fit().
• Predicciones: Utilizar el modelo entrenado para predecir la cantidad que Alex gastará para un número dado de sellos. En el código, predecimos la cantidad para 10 sellos.
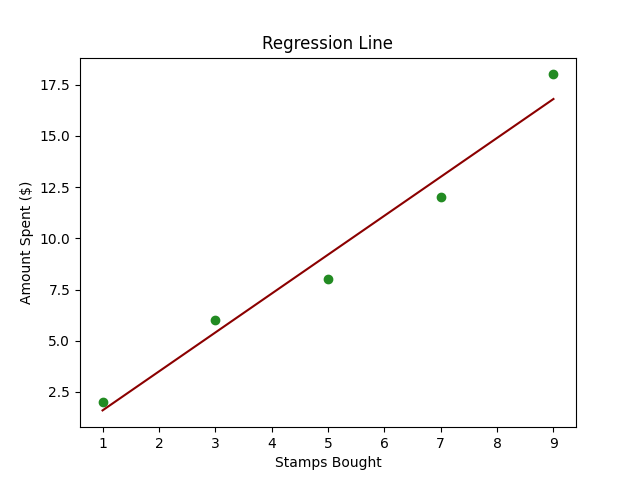
• Gráfica: Graficamos los puntos de datos originales (en azul) y la línea predicha (en rojo) para comprender visualmente la capacidad de predicción de nuestro modelo.
• Mostrar la predicción: Finalmente, imprimimos el gasto predicho para un número específico de sellos (10 en este caso).

‌2.2 Regresión Logística

Otra técnica de Aprendizaje Automático muy popular es la Regresión Logística, que, a pesar de su nombre, en realidad es una técnica de clasificación supervisada.

La regresión logística es un método de Aprendizaje Automático que modela la probabilidad condicional de que ocurra un evento o que una observación pertenezca a una cierta clase, basándose en un conjunto de datos dado de variables independientes.

Cuando la relación entre dos variables es lineal y la variable dependiente es una variable categórica, es posible que desees predecir una variable en forma de probabilidad (un número entre 0 y 1). En estos casos, la Regresión Logística resulta útil.

Esto se debe a que durante el proceso de predicción en la Regresión Logística, el clasificador predice la probabilidad (un valor entre 0 y 1) de que cada observación pertenezca a una cierta clase, normalmente a una de las dos clases de la variable dependiente.

Por ejemplo, si deseas predecir la probabilidad o posibilidad de que un candidato sea elegido o no durante una elección dada la puntuación de popularidad del candidato, los éxitos pasados ​​y otras variables descriptivas sobre ese candidato, puedes usar la Regresión Logística para modelar esta probabilidad.

Entonces, en lugar de predecir la variable de respuesta, la Regresión Logística modela la probabilidad de que Y pertenezca a una categoría específica.

Es similar a la Regresión Lineal con la diferencia de que, en lugar de Y, predice las log odds. En terminología estadística, modelamos la distribución condicional de la respuesta Y, dadas las predictoras X. Por lo tanto, la Regresión Logística ayuda a predecir la probabilidad de que Y pertenezca a una determinada clase (0 y 1) dadas las características P(Y|X=x).

El nombre Logistic en Logistic Regression proviene de la función en la que se basa este enfoque, que es la Función Logística. La Función Logística asegura que para valores demasiado grandes o demasiado pequeños, la probabilidad correspondiente aún se encuentre dentro de los límites [0,1].

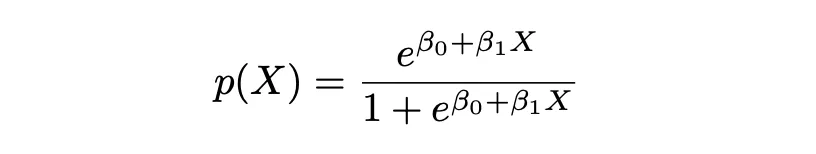
En la ecuación anterior, P(X) representa la probabilidad de que Y pertenezca a cierta clase (0 y 1) dadas las características P(Y|X=x). X representa la variable independiente, β0 es la intersección que es desconocida y constante, β1 es el coeficiente de pendiente o un parámetro correspondiente a la variable X que también es desconocido y constante, similar a la Regresión Lineal. e representa la función exp().

Probabilidades y Logaritmo de las Probabilidades

La Regresión Logística y su técnica de estimación MLE se basan en los términos de Probabilidades y Logaritmo de las Probabilidades. Donde Probabilidades se define de la siguiente manera:

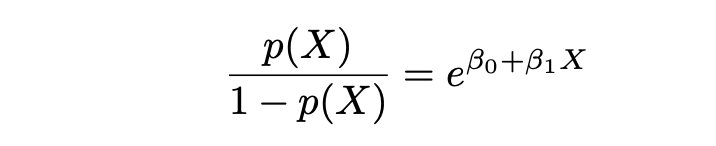
y Logaritmo de las Probabilidades se define de la siguiente manera:

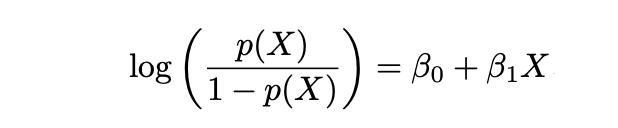
2.2.1 Estimación de Máxima Verosimilitud (MLE)

Mientras que para la Regresión Lineal utilizamos OLS (Mínimos Cuadrados Ordinarios) o LS (Mínimos Cuadrados) como técnica de estimación, para la Regresión Logística debemos usar otra técnica de estimación.

No podemos usar LS en la Regresión Logística para encontrar la mejor línea de ajuste (para realizar la estimación) porque los errores pueden volverse muy grandes o muy pequeños (incluso negativos), mientras que en el caso de la Regresión Logística pretendemos obtener un valor predicho en [0,1].

Entonces, para la Regresión Logística utilizamos la técnica MLE, donde la función de verosimilitud calcula la probabilidad de observar el resultado dadas los datos de entrada y el modelo. Esta función luego se optimiza para encontrar el conjunto de parámetros que produce la mayor suma de verosimilitud sobre el conjunto de datos de entrenamiento.

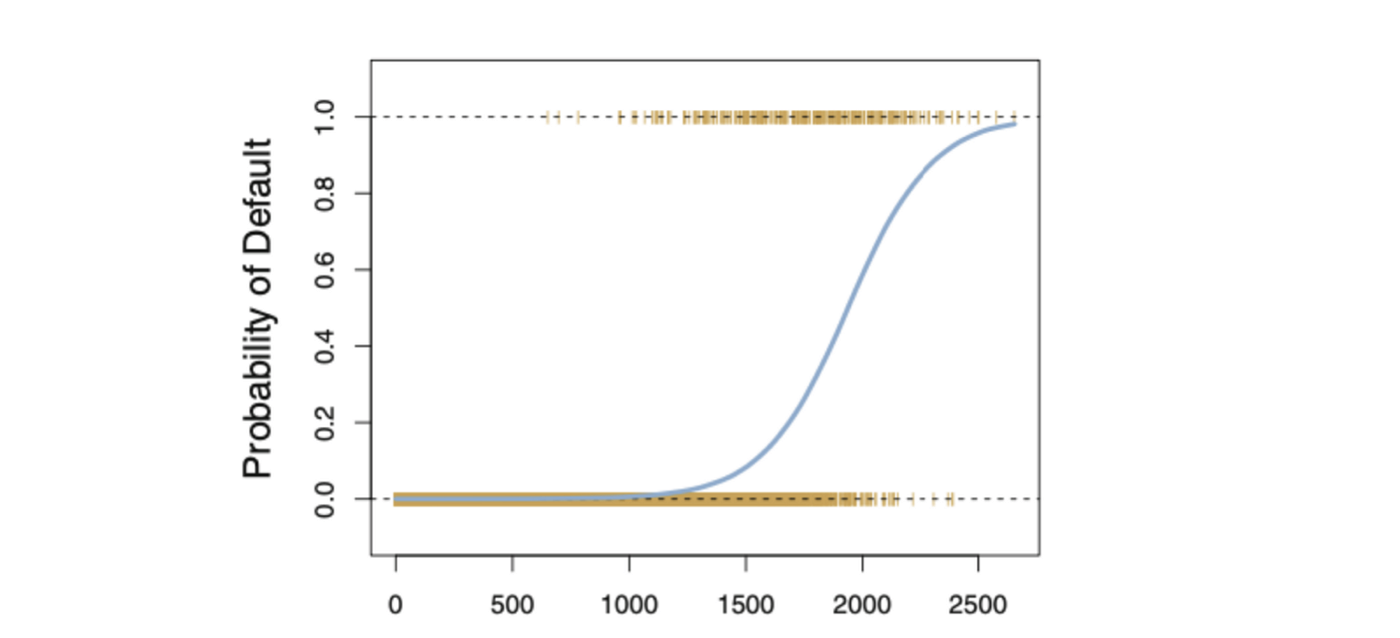
La función logística siempre producirá una curva en forma de S como la de arriba, independientemente del valor de la variable independiente X, lo que resulta en estimaciones sensatas la mayor parte del tiempo.

2.2.2 Función(es) de Verosimilitud de la Regresión Logística

La función de verosimilitud puede expresarse de la siguiente manera:

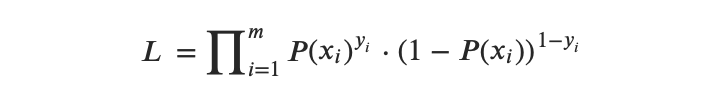
Entonces, la función de logaritmo de verosimilitud puede expresarse de la siguiente manera:

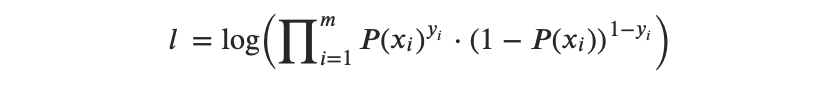
o, después de la transformación de multiplicadores a suma, obtenemos:

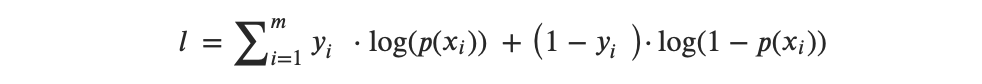
Entonces, la idea detrás de la MLE es encontrar un conjunto de estimaciones que maximice esta función de verosimilitud.

• Paso 1: Proyectar los puntos de datos en una línea candidata que produzca un valor de logaritmo de probabilidad (log odds) de la muestra.
• Paso 2: Transformar el logaritmo de probabilidad de la muestra a probabilidades de la muestra utilizando la siguiente fórmula:

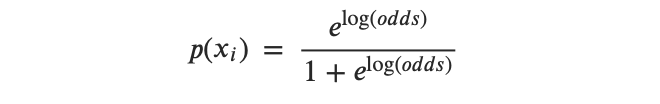
• Paso 3: Obtén la probabilidad general o la probabilidad logarítmica general.
• Paso 4: Gira la línea de logaritmo (odds) una y otra vez, hasta encontrar el logaritmo (odds) óptimo que maximice la probabilidad general.

2.2.3 Valor de corte en la Regresión Logística

Si planeas usar Regresión Logística para obtener un valor binario {0,1} al final, necesitas un punto de corte para transformar los valores estimados por observación dentro del rango de [0,1] a un valor de 0 o 1.

Dependiendo de tu caso individual, puedes elegir un punto de corte correspondiente, pero un punto de corte popular es 0.5. En este caso, todas las observaciones con un valor predicho menor que 0.5 se asignarán a la clase 0 y las observaciones con un valor predicho mayor o igual que 0.5 se asignarán a la clase 1.

2.2.4 Métricas de rendimiento en la Regresión Logística

Dado que la Regresión Logística es un método de clasificación, se pueden utilizar métricas comunes de clasificación como recall, precisión y medida F-1. Pero también existe un sistema de métricas que se utiliza comúnmente para evaluar el rendimiento del modelo de Regresión Logística, llamado Deviance.

2.2.5 Regresión Logística en Python

Jenny es una ávida lectora de libros. Jenny lee libros de diferentes géneros y lleva un pequeño diario donde anota el número de páginas y si le gustó el libro (Sí o No).

Vemos un patrón: Jenny habitualmente disfruta de libros que no sean ni demasiado cortos ni demasiado largos. ¿Podemos predecir si a Jenny le gustará un libro en función de su número de páginas? ¡Aquí es donde la Regresión Logística puede ayudarnos!

En términos técnicos, estamos tratando de predecir un resultado binario (gustar/no gustar) basado en una variable independiente (número de páginas).

Aquí tienes un ejemplo simplificado en Python que utiliza scikit-learn para implementar la Regresión Logística:

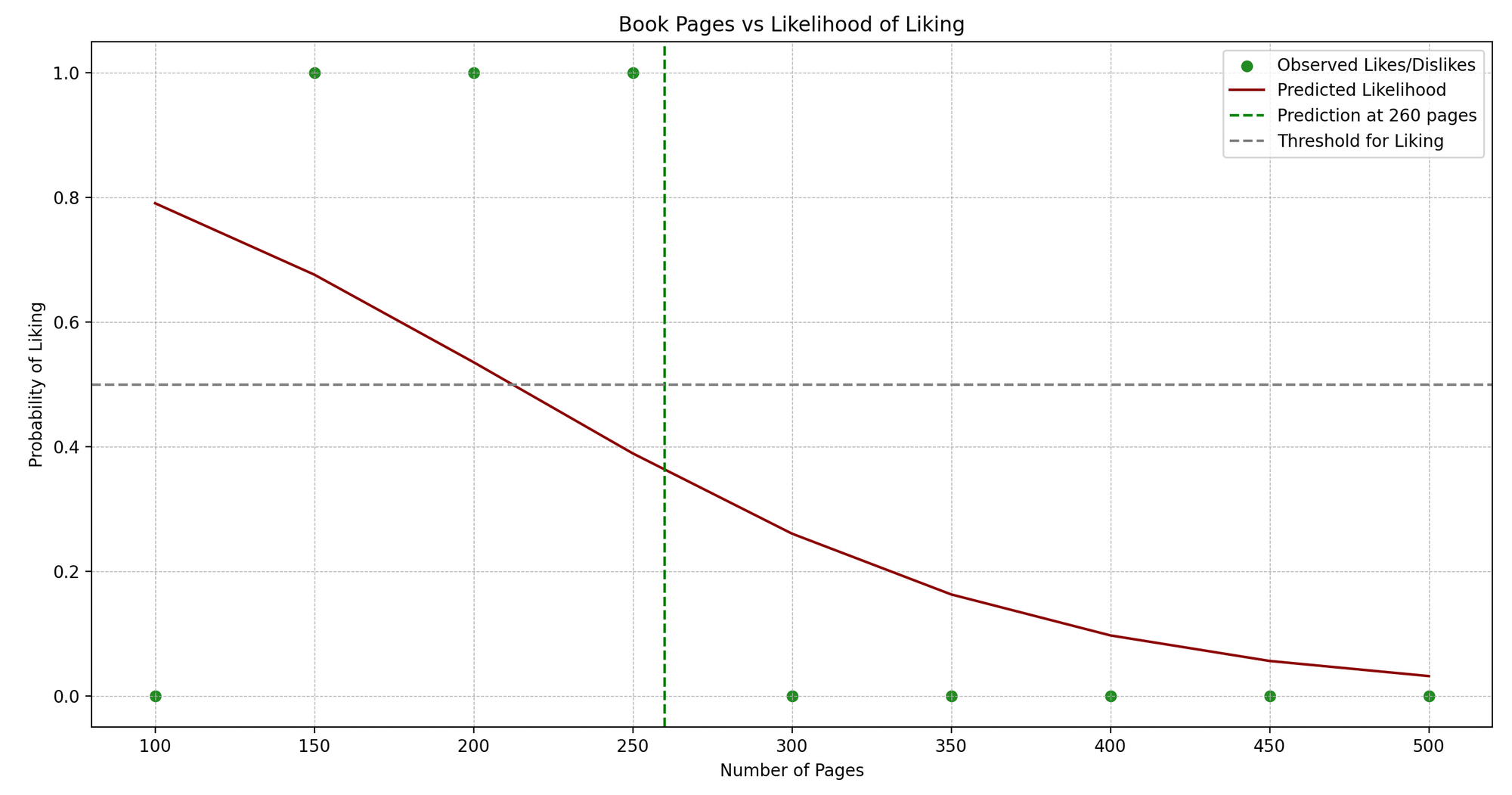
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import accuracy_score# Datos de muestra.pages = np.array([100, 150, 200, 250, 300, 350, 400, 450, 500]).reshape(-1, 1)likes = np.array([0, 1, 1, 1, 0, 0, 0, 0, 0])  # 1: Gusta, 0: No gusta# Crear un modelo de Regresión Logísticamodelo = LogisticRegression()# Entrenar el modelo.modelo.fit(pages, likes)# Prediccionespredict_book_pages = 260predicted_like = modelo.predict([[predict_book_pages]])# Graficarplt.scatter(pages, likes, color='forestgreen')plt.plot(pages, modelo.predict_proba(pages)[:, 1], color='darkred')plt.title('Número de Páginas del Libro vs Gusto/No Gusto')plt.xlabel('Número de Páginas')plt.ylabel('Probabilidad de Gustar')plt.axvline(x=predict_book_pages, color='green', linestyle='--')plt.axhline(y=0.5, color='grey', linestyle='--')plt.show()# Mostrar la Prediccióncprint(f"Jenny {'gustará' if predicted_like[0] == 1 else 'no gustará'} un libro de {predict_book_pages} páginas.")

• Datos de muestra: pages representa el número de páginas de los libros que Jenny ha leído, y likes representa si le gustaron (1 para gusta, 0 para no gusta).
• Creando y entrenando el modelo: Instanciamos LogisticRegression() y entrenamos el modelo usando .fit() con nuestros datos.
• Predicciones: Predecimos si a Jenny le gustará un libro con un número de páginas particular (260 en este ejemplo).
• Graficando: Visualizamos los puntos de datos originales (en azul) y la curva de probabilidad predicha (en rojo). La línea punteada verde representa el número de página que estamos prediciendo, y la línea punteada gris indica el umbral (0.5) por encima del cual predecimos un “gusto”.
• Mostrando la Predicción: Imprimimos si a Jenny le gustará un libro con el número de páginas dado basado en la predicción de nuestro modelo.

‌2.3 Análisis Discriminante Lineal (LDA)

Otra técnica de clasificación, estrechamente relacionada con la Regresión Logística, es el Análisis Discriminante Lineal (LDA). Mientras que la Regresión Logística se usa generalmente para modelar la probabilidad de que una observación pertenezca a una clase de la variable de resultado con 2 categorías, LDA se usa generalmente para modelar la probabilidad de que una observación pertenezca a una clase de la variable de resultado con 3 o más categorías.

LDA ofrece un enfoque alternativo para modelar la probabilidad condicional de la variable de resultado dada ese conjunto de predictores que aborda los problemas de la Regresión Logística. Modela la distribución de los predictores X por separado en cada una de las clases de respuesta (es decir, dada Y), y luego utiliza el teorema de Bayes para intercambiar estos dos términos y obtener las estimaciones de Pr(Y = k|X = x).

Es importante tener en cuenta que en el caso de LDA se asume que estas distribuciones son normales. Resulta que el modelo es muy similar en forma a la regresión logística. En la ecuación aquí:

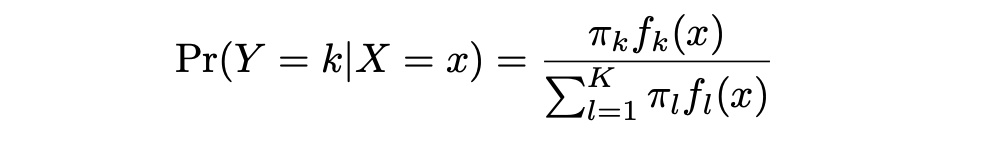
π_k representa la probabilidad previa total de que una observación elegida al azar provenga de la k-ésima clase. f_k(x), que es igual a Pr(X = x|Y = k), representa la probabilidad posterior, y es la función de densidad de X para una observación que proviene de la k-ésima clase (función de densidad de los predictores).

Esta es la probabilidad de que X=x dada la observación es de una clase determinada. En otras palabras, es la probabilidad de que la observación pertenezca a la k-ésima clase, dado el valor del predictor para esa observación.

Suponiendo que f_k(x) es una distribución Normal o Gaussiana, la densidad normal toma la siguiente forma (en un solo-dimensionamiento normal):

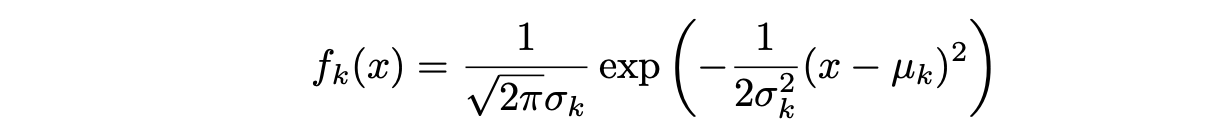
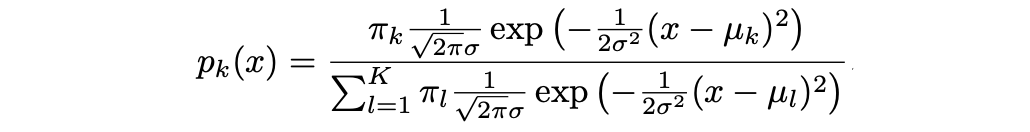
donde μ_k y σ_k² son los parámetros de media y varianza para la k-ésima clase. Suponiendo que σ_¹² = · · · = σ_K² (hay un término de varianza compartida entre todas las K clases, que denotamos como σ2).

Luego, LDA aproxima el clasificador de Bayes utilizando las siguientes estimaciones para πk, μk y σ2:

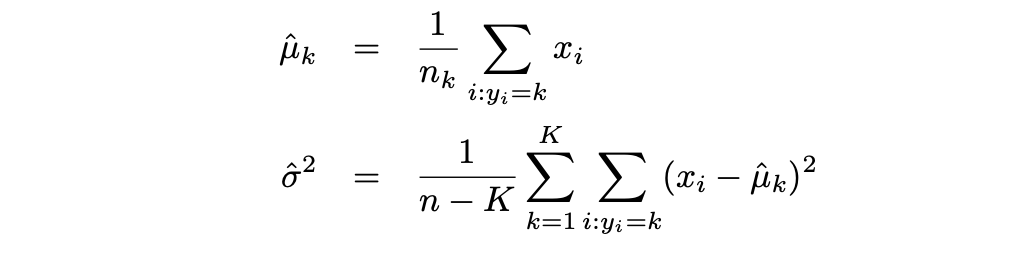
Mientras que la Regresión Logística se usa generalmente para modelar la probabilidad de que una observación pertenezca a una clase de la variable de resultado con 2 categorías, LDA se usa generalmente para modelar la probabilidad de que una observación pertenezca a una clase de la variable de resultado con 3 o más categorías.

2.3.1 Análisis Discriminante Lineal en Python

Imagina a Sarah, a quien le encanta cocinar y probar diferentes frutas. Ella nota que las frutas que le gustan suelen tener tamaños y niveles de dulzura específicos.

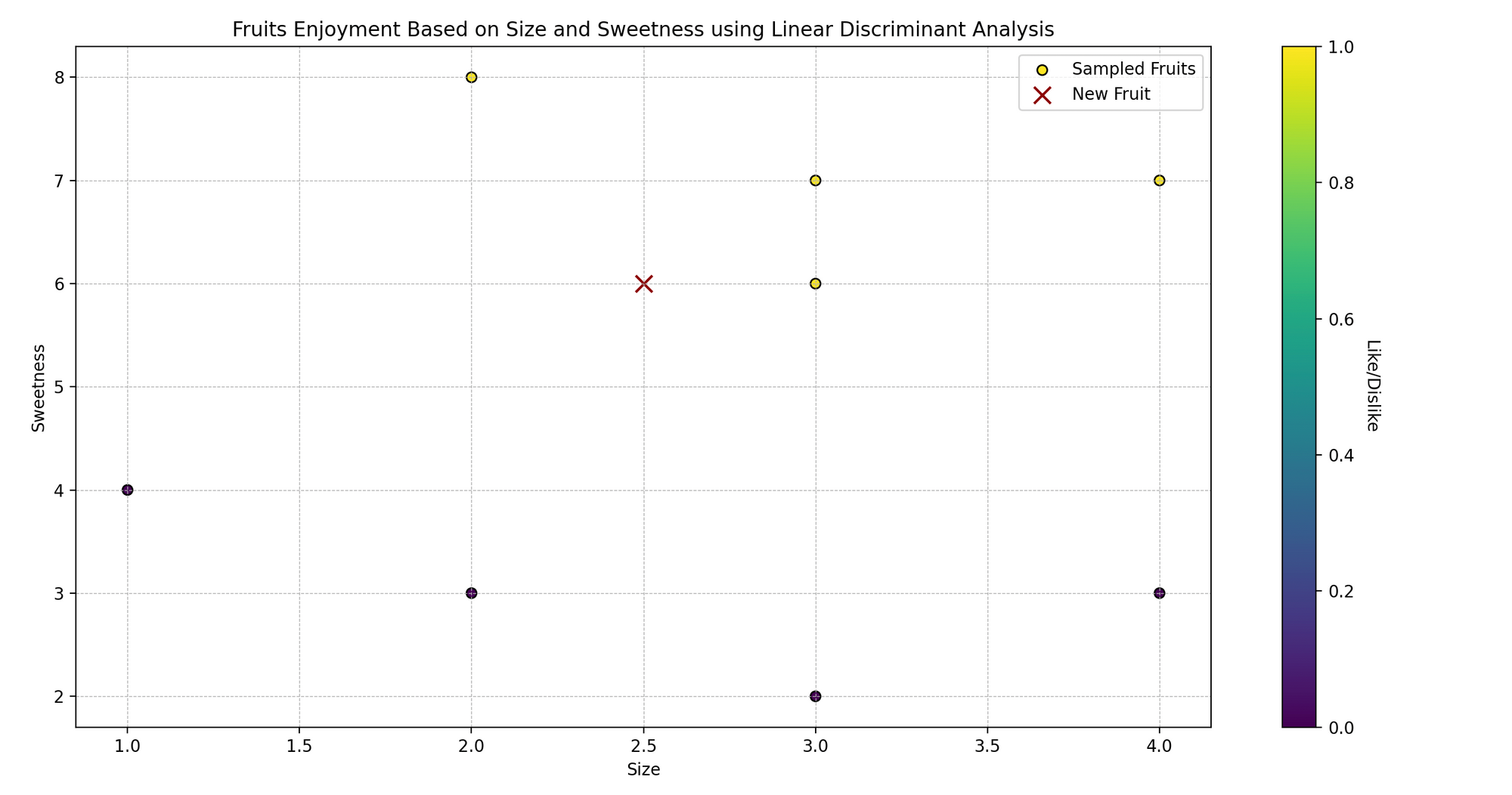
Ahora, Sarah está curiosa: ¿puede predecir si le gustará una fruta basándose en su tamaño y dulzura? Utilicemos el Análisis Discriminante Lineal (LDA) para ayudarla a predecir si le gustarán ciertas frutas o no.

En lenguaje técnico, estamos tratando de clasificar las frutas (gustar/no gustar) en función de dos variables predictoras (tamaño y dulzura).

import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# Datos de muestra
# [tamaño, dulzura]
caracteristicas_frutas = np.array([[3, 7], [2, 8], [3, 6], [4, 7], [1, 4], [2, 3], [3, 2], [4, 3]])
gustos_frutas = np.array([1, 1, 1, 1, 0, 0, 0, 0])  # 1: Gusta, 0: No gusta

# Creando un modelo LDA
modelo = LinearDiscriminantAnalysis()

# Entrenando el modelo
modelo.fit(caracteristicas_frutas, gustos_frutas)

# Predicción
nueva_fruta = np.array([[2.5, 6]])  # [tamaño, dulzura]
gusto_predicho = modelo.predict(nueva_fruta)

# Visualización de datos
plt.scatter(caracteristicas_frutas[:, 0], caracteristicas_frutas[:, 1], c=gustos_frutas, cmap='viridis', marker='o')
plt.scatter(nueva_fruta[:, 0], nueva_fruta[:, 1], color='darkred', marker='x')
plt.title('Disfrute de las Frutas Basado en Tamaño y Dulzura')
plt.xlabel('Tamaño')
plt.ylabel('Dulzura')
plt.show()

# Mostrando la predicción
print(f"Sarah {'gustará' if gusto_predicho[0] == 1 else 'no gustará'} una fruta de tamaño {nueva_fruta[0, 0]} y dulzura {nueva_fruta[0, 1]}.")

• Datos de muestra: caracteristicas_frutas contiene dos características: tamaño y dulzura de las frutas, y gustos_frutas representa si a Sarah le gustan (1 para gustar, 0 para no gustar).
• Creando y entrenando el modelo: Instanciamos LinearDiscriminantAnalysis() y lo entrenamos usando .fit() con nuestros datos de muestra.
• Predicción: Predecimos si a Sarah le gustará una fruta con un tamaño y nivel de dulzura específicos ([2.5, 6] en este ejemplo).
• Visualización: Visualizamos los puntos de datos originales, codificados por colores según si a Sarah le gusta (amarillo) o no le gusta (morado), y marcamos la nueva fruta con una equis (x) roja.
• Mostrando la predicción: Mostramos si a Sarah le gustará una fruta con el tamaño y nivel de dulzura dados, según la predicción de nuestro modelo.

2.4 Regresión Logística vs LDA

La regresión logística es un enfoque popular para realizar clasificaciones cuando hay dos clases. Pero cuando las clases están bien separadas o el número de clases es superior a 2, las estimaciones de los parámetros del modelo de regresión logística son sorprendentemente inestables.

A diferencia de la regresión logística, LDA no sufre de este problema de inestabilidad cuando el número de clases es más de 2. Si n es pequeño y la distribución de los predictores X es aproximadamente normal en cada una de las clases, LDA es nuevamente más estable que el modelo de regresión logística.

2.5 Naïve Bayes

Otro método de clasificación que se basa en la Regla de Bayes, al igual que LDA, es el enfoque de clasificación de Naïve Bayes. Para obtener más información sobre el Teorema de Bayes, la Regla de Bayes y un ejemplo correspondiente, puedes leer estos artículos.

Al igual que en la regresión logística, puedes utilizar el enfoque de Naïve Bayes para clasificar observaciones en una de las dos clases (0 o 1).

La idea detrás de este método es calcular la probabilidad de que una observación pertenezca a una clase dada la probabilidad previa para esa clase y la probabilidad condicional de cada valor de la característica dada para una clase dada. Es decir:

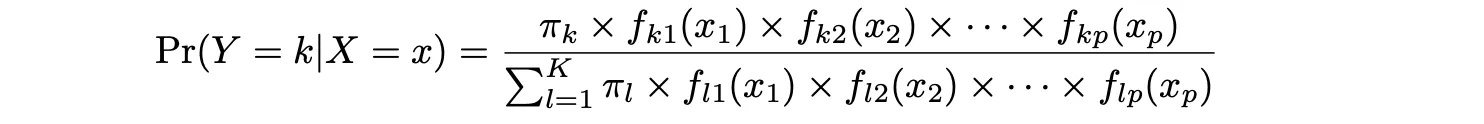
donde Y representa la clase de la observación, k es la k-ésima clase y x1, …, xn representan las características 1 hasta la característica n, respectivamente. f_k(x) = Pr(X = x|Y = k) representa la probabilidad a posteriori, que al igual que en el caso de LDA es la función de densidad de X para una observación que proviene de la k-ésima clase (función de densidad de los predictores).

Si comparas la expresión anterior con la que viste para LDA, verás algunas similitudes.

En LDA, hacemos una suposición muy importante y fuerte con fines de simplificación: es decir, que f_k es la función de densidad para una variable aleatoria normal multivariante con media μ_k específica de la clase y matriz de covarianza compartida Sigma Σ.

Esta suposición ayuda a reemplazar el desafiante problema de estimar K funciones de densidad p-dimensionales con el problema mucho más simple, que es estimar vectores de medias p-dimensionales de K y matrices de covarianza (p × p)-dimensionales.

En el caso del clasificador Naïve Bayes, utiliza un enfoque diferente para estimar f_1 (x), . . . , f_K(x). En lugar de hacer una suposición de que estas funciones pertenecen a una familia particular de distribuciones (por ejemplo, normal o normal multivariante), en su lugar hacemos una sola suposición: dentro de la k-ésima clase, los p predictores son independientes. Es decir:

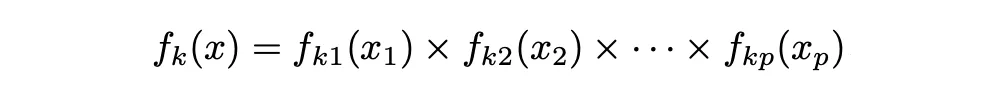
Así que el clasificador de Bayes asume que el valor de una variable o característica particular es independiente del valor de cualquier otra variable (no correlacionada), dado la variable de clase/etiqueta.

Por ejemplo, una fruta podría considerarse como plátano si es amarilla, tiene forma ovalada y mide alrededor de 5-10 cm de largo. Entonces, el clasificador Naïve Bayes considera que cada una de estas diversas características de la fruta contribuyen de forma independiente a la probabilidad de que esta fruta sea un plátano, independientemente de cualquier posible correlación entre las características de color, forma y longitud.

Estimación de Naïve Bayes

Al igual que en la Regresión Logística, en el caso del enfoque de clasificación Naïve Bayes utilizamos la Estimación de Máxima Verosimilitud (MLE) como técnica de estimación. Hay un gran artículo que proporciona un resumen detallado y conciso para este enfoque con un ejemplo correspondiente que puedes encontrar aquí.

2.5.1 Naïve Bayes en Python

Tom es un entusiasta del cine que ve películas de diferentes géneros y registra sus comentarios, si le gustaron o no. Ha notado que si le gusta una película puede depender de dos aspectos: la duración de la película y su género. ¿Podemos predecir si a Tom le va a gustar una película basándonos en estas dos características usando Naïve Bayes?

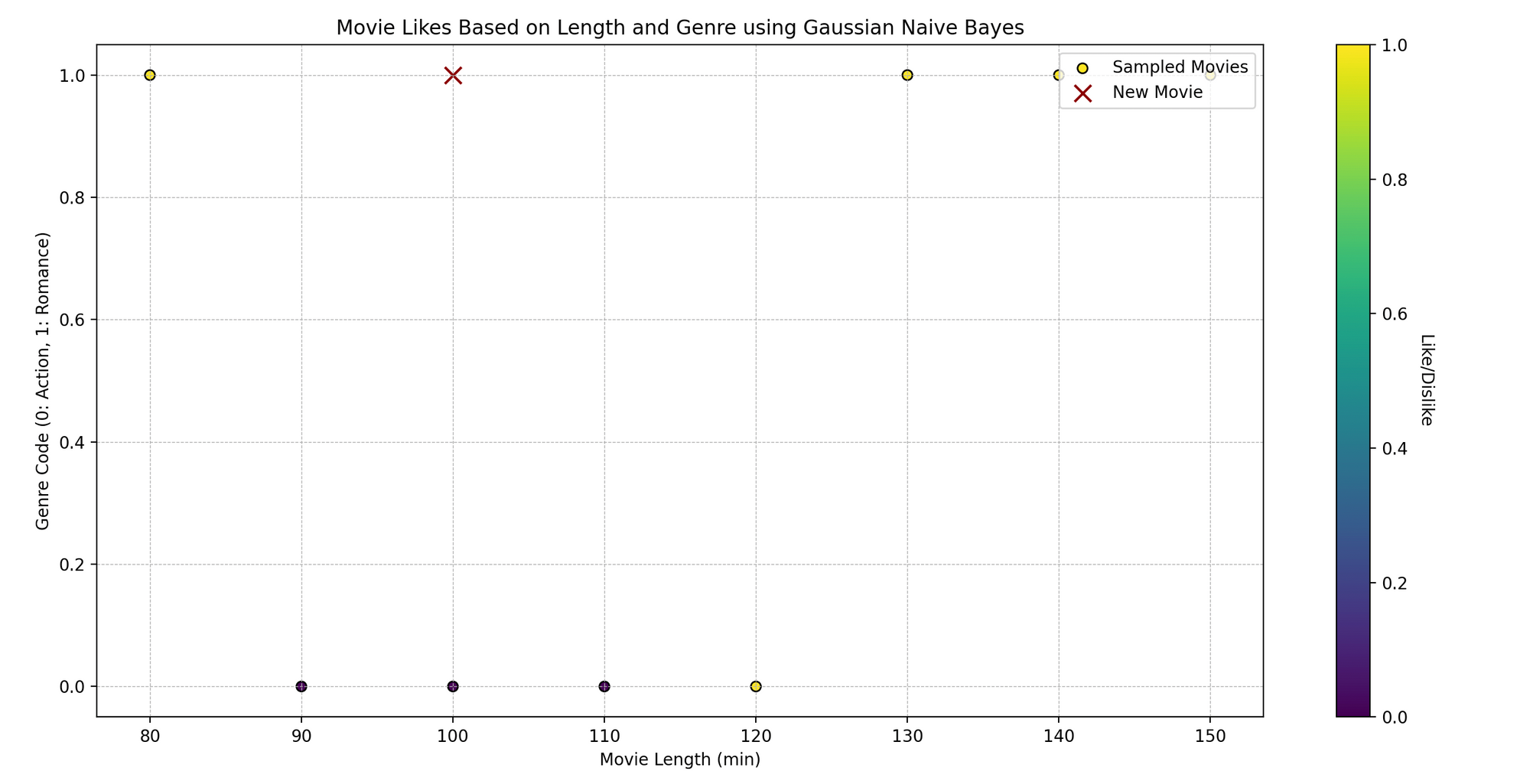
Técnicamente, queremos predecir un resultado binario (gustar/no gustar) basado en las variables independientes (duración de la película y género).

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.naive_bayes import GaussianNB# Datos de muestra# [duración_pelicula, codigo_genero] (asumiendo que el género está codificado como: 0 para Acción, 1 para Romance, etc.)caracteristicas_peliculas = np.array([[120, 0], [150, 1], [90, 0], [140, 1], [100, 0], [80, 1], [110, 0], [130, 1]])gusta_peliculas = np.array([1, 1, 0, 1, 0, 1, 0, 1])  # 1: Gusta, 0: No gusta# Creando un modelo Naive Bayesmodelo = GaussianNB()# Entrenando el Modelomodelo.fit(caracteristicas_peliculas, gusta_peliculas)# Prediccióncueva_pelicula = np.array([[100, 1]])  # [duración_pelicula, codigo_genero]gusta_predicha = modelo.predict(cueva_pelicula)# Graficandoplt.scatter(caracteristicas_peliculas[:, 0], caracteristicas_peliculas[:, 1], c=gusta_peliculas, cmap='viridis', marker='o')plt.scatter(cueva_pelicula[:, 0], cueva_pelicula[:, 1], color='darkred', marker='x')plt.title('Gustos de Películas basado en Duración y Código de Género')plt.xlabel('Duración de la Película (min)')plt.ylabel('Código de Género')plt.show()# Mostrando la Predicciónprint(f"Tom {'gustará' if gusta_predicha[0] == 1 else 'no gustará'} una película de {cueva_pelicula[0, 0]} minutos de duración y código de género {cueva_pelicula[0, 1]}.")

• Datos de muestra: caracteristicas_peliculas contiene dos características: duración de la película y género (codificado como números), mientras que gusta_peliculas indica si a Tom le gustan (1) o no (0).
• Creación y entrenamiento del modelo: Instanciamos GaussianNB() (un clasificador Naïve Bayes que asume una distribución gaussiana de los datos) y lo entrenamos con .fit() utilizando nuestros datos.
• Predicción: Predecimos si a Tom le gustará una nueva película, dada su duración y código de género ([100, 1] en este caso).
• Graficación: Visualizamos los puntos de datos originales, con colores según si a Tom le gusta (amarillo) o no le gusta (morado). La ‘x’ roja representa la nueva película.
• Mostrando la predicción: Imprimimos si a Tom le gustará una película de la duración y código de género dados, según la predicción de nuestro modelo.

2.6 Naïve Bayes vs Regresión Logística

El Clasificador Naïve Bayes ha demostrado ser más rápido y tiene un sesgo más alto y una varianza más baja. La regresión logística tiene un sesgo bajo y una varianza más alta. Dependiendo de su caso individual y del trade-off sesgo-varianza, puede elegir el enfoque correspondiente.

2.7 Árboles de Decisión

Los árboles de decisión son un método de aprendizaje automático supervisado y no paramétrico utilizado tanto para la clasificación como para la regresión. La idea es crear un modelo que prediga el valor de una variable objetivo aprendiendo reglas de decisión simples a partir de los predictores de los datos.

A diferencia de la Regresión Lineal o la Regresión Logística, los árboles de decisión son modelos simples y útiles cuando se sospecha que la relación entre las variables independientes y la variable dependiente es no lineal.

Los métodos basados en árboles estratifican o dividen el espacio de los predictores en regiones más pequeñas. La idea detrás de la construcción de árboles de decisión es dividir el espacio de los predictores en regiones distintas y mutuamente excluyentes X1, X2,….. , Xp → R_1, R_2, …, R_N donde las regiones tienen forma de cajas o rectángulos. Estas regiones se encuentran mediante una división binaria recursiva, ya que minimizar el error cuadrático residual no es factible. Este enfoque a menudo se denomina enfoque ávido.

Los árboles de decisión se construyen dividiendo de arriba hacia abajo. Entonces, al principio, todas las observaciones pertenecen a una sola región. Luego, el modelo divide sucesivamente el espacio de los predictores. Cada división se indica mediante dos nuevas ramas más abajo en el árbol.

Este enfoque a veces se llama ávido porque en cada paso del proceso de construcción del árbol, se realiza la mejor división en ese paso en particular, en lugar de anticipar y elegir una división que conducirá a un mejor árbol en algún paso futuro.

Criterios de detención

Hay algunos criterios comunes de detención utilizados al construir árboles de decisión:

• Número mínimo de observaciones en la hoja.
• Número mínimo de muestras para una división de nodos.
• Profundidad máxima del árbol (profundidad vertical).
• Número máximo de nodos terminales.
• Número máximo de características a considerar para la división.

Por ejemplo, repita este proceso de división hasta que ninguna región contenga más de 100 observaciones. Vamos a profundizar

1. Número mínimo de observaciones en la hoja: Si una división propuesta resulta en un nodo hoja con menos de un número definido de observaciones, esa división puede descartarse. Esto evita que el árbol se vuelva demasiado complejo.

2. Número mínimo de muestras para una división de nodos: Para proceder con una división de nodos, el nodo debe tener al menos esta cantidad de muestras. Esto garantiza que haya una cantidad significativa de datos para justificar la división.

3. Profundidad máxima del árbol (profundidad vertical): Esto limita cuántas veces puede dividirse un árbol. Es como decirle al árbol cuántas preguntas puede hacer sobre los datos antes de tomar una decisión.

4. Número máximo de nodos terminales: Este es el número total de nodos finales (o hojas) que el árbol puede tener.

5. Número máximo de características a considerar para la división: Para cada división, el algoritmo considera solo un subconjunto de características. Esto puede acelerar el entrenamiento y ayudar en la generalización.

Al construir un árbol de decisión, especialmente cuando se trata de un gran número de características, el árbol puede volverse demasiado grande con demasiadas hojas. Esto afectará la interpretación del modelo y potencialmente podría resultar en un problema de sobreadaptación . Por lo tanto, elegir un buen criterio de detención es fundamental para la interpretación y el rendimiento del modelo.

Índice RSS/Gini/Entropía/Pureza de nodo

Cuando construimos el árbol, utilizamos el RSS (para árboles de regresión) y el índice Gini/entropía (para árboles de clasificación) para elegir el predictor y el valor para dividir las regiones. Tanto el índice Gini como la entropía se llaman a menudo medidas de pureza de nodo porque describen qué tan puros son los nodos hoja de los árboles.

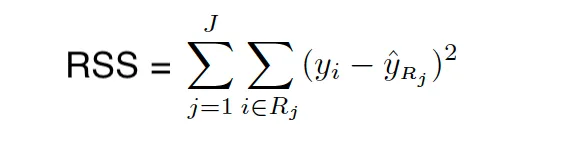
Índice Gini

El índice Gini mide la varianza total entre K clases. Toma un valor pequeño cuando todas las tasas de error de clase son 1 o 0. Por eso se le llama una medida de pureza de nodo, el índice Gini toma valores pequeños cuando los nodos del árbol contienen predominantemente observaciones de la misma clase.

El índice Gini se define de la siguiente manera:

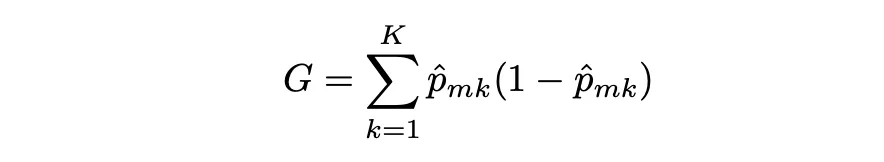
dónde pˆmk representa la proporción de observaciones de entrenamiento en la región m que pertenecen a la clase k.

Entropía

La entropía es otra medida de pureza de nodo, y al igual que el índice Gini, la entropía toma un valor pequeño si el nodo m es puro. De hecho, el índice Gini y la entropía son medidas numéricas bastante similares y se pueden expresar de la siguiente manera:

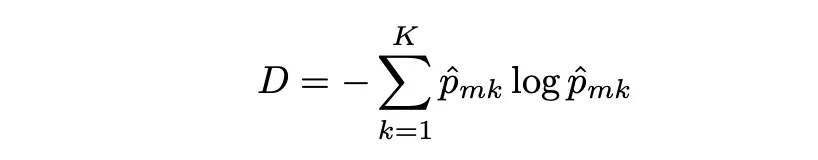
Ejemplo de clasificación de árbol de decisiones

Veamos un ejemplo en el que tenemos tres características que describen el comportamiento pasado de los consumidores:

• Recencia (¿Qué tan reciente fue la última compra del cliente?)
• Monetario (¿Cuánto dinero gastó el cliente en un período determinado?)
• Frecuencia (¿Con qué frecuencia hizo una compra este cliente en un período determinado?)

Utilizaremos la versión de clasificación del árbol de decisiones para clasificar a los clientes en 1 de las 3 clases (Bueno: 1, Mejor: 2 y Excelente: 3), según las características que describen el comportamiento del cliente.

En el siguiente árbol, donde utilizamos el índice Gini como medida de pureza, vemos que la primera característica que parece ser la más importante es la Recencia. Veamos el árbol y luego lo interpretaremos:

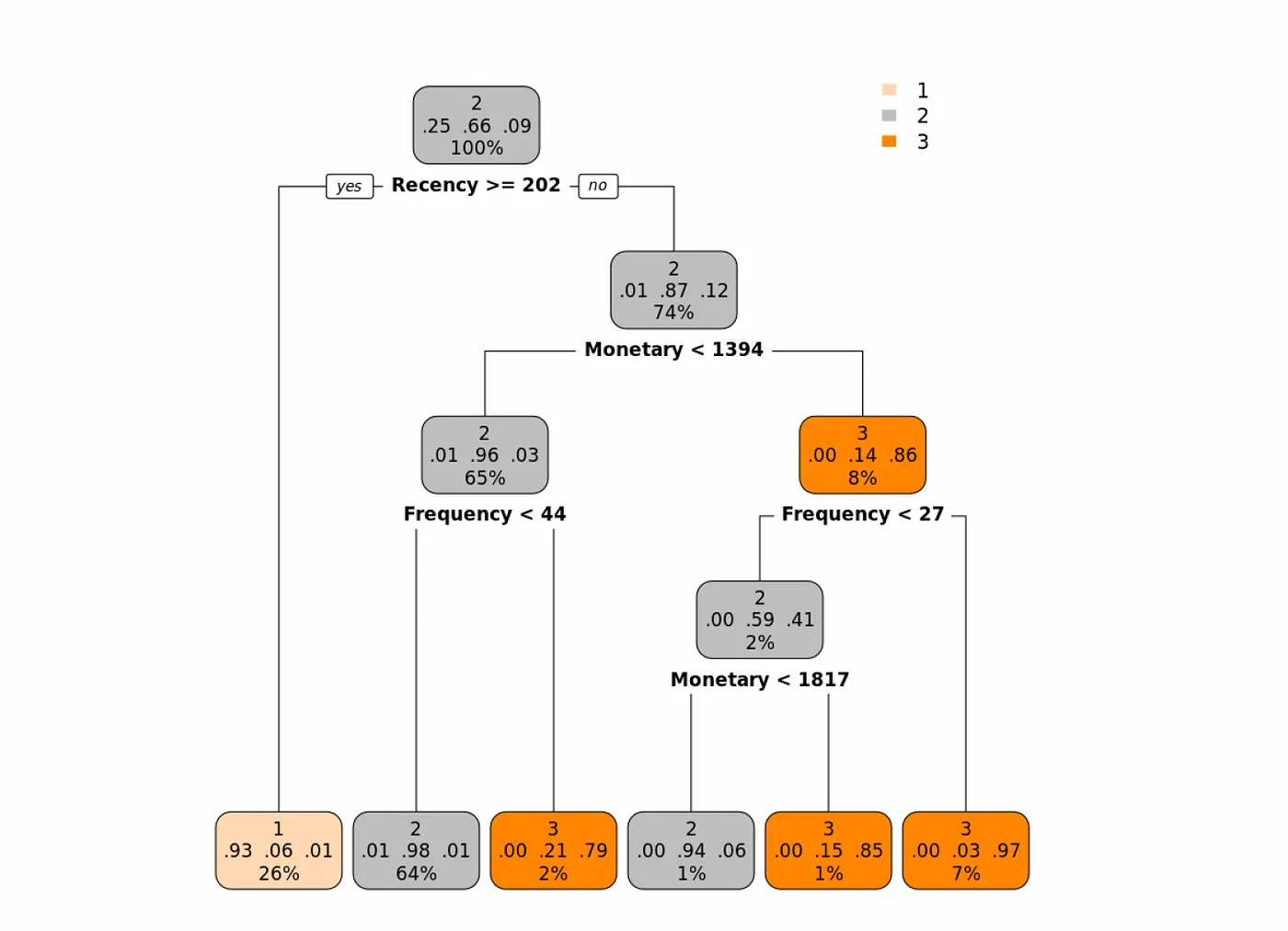
Los clientes que tienen una recencia de 202 o más (la última vez que hicieron una compra > 202 días atrás), entonces la probabilidad de que esta observación se asigne a la clase 1 es del 93% (básicamente, podemos etiquetar a esos clientes como clientes de clase Buena).

Para los clientes con Recencia menor a 202 (hicieron una compra reciente), observamos su valor Monetario y si es menor a 1394, luego observamos su Frecuencia. Si la Frecuencia es menor a 44, entonces podemos etiquetar a esta clase de clientes como Mejor o (clase 2). Y así sucesivamente.

Implementación de árboles de decisión en Python

Alex está intrigado por la relación entre el número de horas estudiadas y las calificaciones obtenidas por los estudiantes. Alex recopiló datos de sus compañeros sobre las horas de estudio y las calificaciones respectivas de los exámenes.

Se pregunta: ¿podemos predecir la calificación de un estudiante en función de las horas que estudia? Vamos a aprovechar el árbol de decisión de regresión para descubrir esto.

Técnicamente, estamos prediciendo un resultado continuo (calificación del examen) en función de una variable independiente (horas de estudio).

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.tree import DecisionTreeRegressor, plot_tree# Datos de muestra# [horas_estudiadas]horas_estudio = np.array([1, 2, 3, 4, 5, 6, 7, 8]).reshape(-1, 1)calificaciones_examen = np.array([50, 55, 70, 80, 85, 90, 92, 98])# Creación de un modelo de regresión de árbol de decisionesmodelo = DecisionTreeRegressor(max_depth=3)# Entrenamiento del modelomodel.fit(horas_estudio, calificaciones_examen)# Predicciónnueva_hora_estudio = np.array([[5.5]])  # ejemplo de horas estudiadascalificacion_predicha = model.predict(nueva_hora_estudio)# Graficando el árbol de decisionesplt.figure(figsize=(12, 8))plot_tree(model, filled=True, rounded=True, feature_names=["Horas de estudio"])plt.title('Árbol de Regresión de Árbol de Decisiones')plt.show()# Graficando Horas de estudio vs. Calificaciones de exámenesplt.scatter(horas_estudio, calificaciones_examen, color='darkred')plt.plot(np.sort(horas_estudio, axis=0), model.predict(np.sort(horas_estudio, axis=0)), color='orange')plt.scatter(nueva_hora_estudio, calificacion_predicha, color='green')plt.title('Horas de estudio vs. Calificaciones de exámenes')plt.xlabel('Horas de estudio')plt.ylabel('Calificaciones de exámenes')plt.grid(True)plt.show()# Mostrando la Predicciónprint(f"Calificación de exámen predicha para {nueva_hora_estudio[0, 0]} horas de estudio: {calificacion_predicha[0]:.2f}.")

• Datos de muestra: study_hours contiene las horas estudiadas y test_scores contiene las puntuaciones de los exámenes correspondientes.
• Creación y entrenamiento del modelo: Creamos un DecisionTreeRegressor con una profundidad máxima especificada (para evitar el sobreajuste) y lo entrenamos con .fit() utilizando nuestros datos.
• Representación gráfica del árbol de decisiones: plot_tree nos ayuda a visualizar el proceso de toma de decisiones del modelo, representando las divisiones basadas en las horas de estudio.
• Predicción y representación gráfica: Predecimos la puntuación del examen para un nuevo valor de horas de estudio (5.5 en este ejemplo), visualizamos los puntos de datos originales, las puntuaciones predichas por el árbol de decisiones y la nueva predicción.

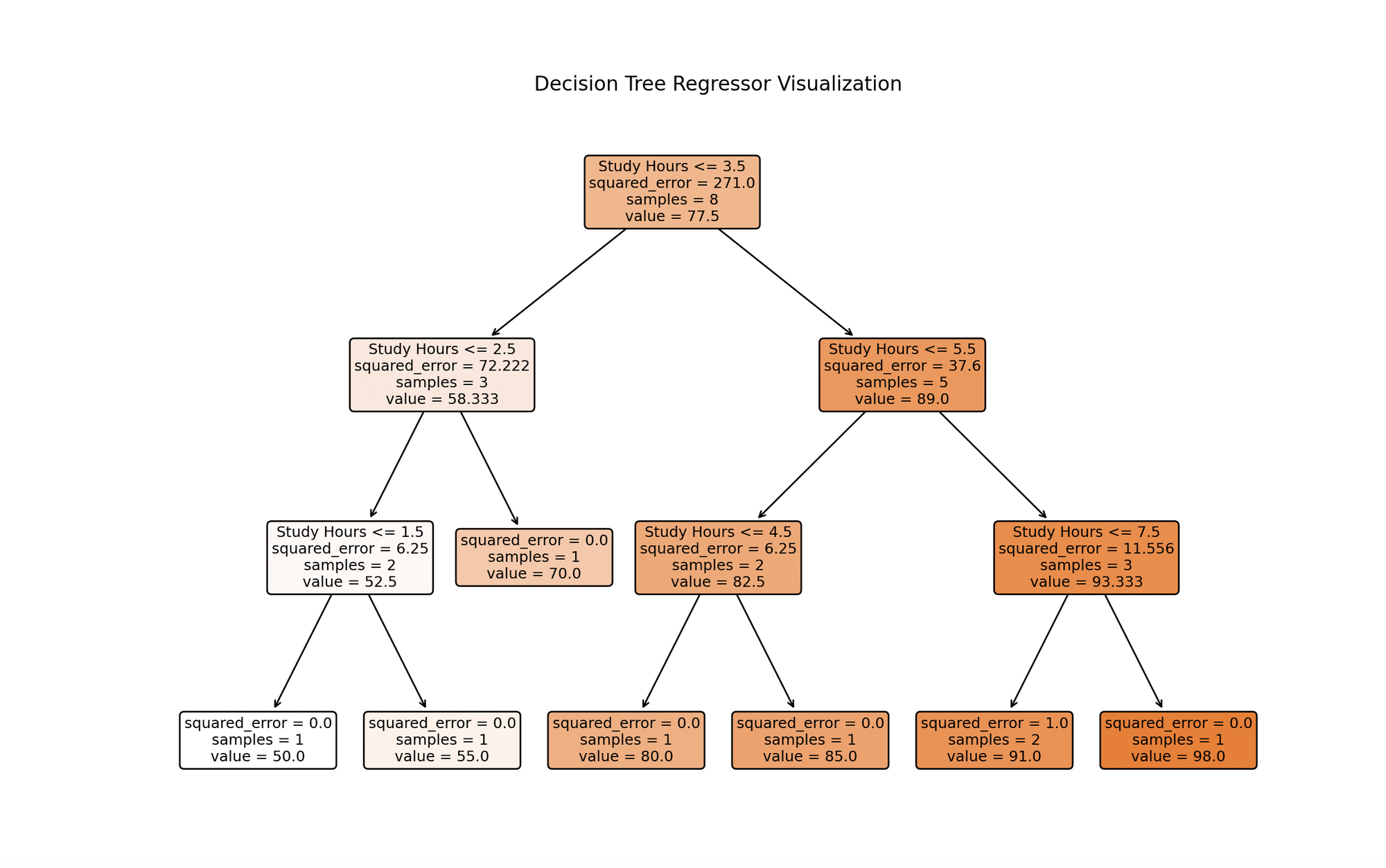
La visualización representa un modelo de árbol de decisiones entrenado con datos de horas de estudio. Cada nodo representa una decisión basada en las horas de estudio, ramificándose desde la raíz superior en función de las condiciones que mejor pronostican las puntuaciones de los exámenes. El proceso continúa hasta alcanzar una profundidad máxima o no se realicen más divisiones significativas. Los nodos de hoja en la parte inferior dan las predicciones finales, que para los árboles de regresión son el promedio de los valores objetivo para las instancias de entrenamiento que alcanzan esa hoja. Esta visualización destaca el enfoque predictivo del modelo y la influencia significativa de las horas de estudio en las puntuaciones de los exámenes.

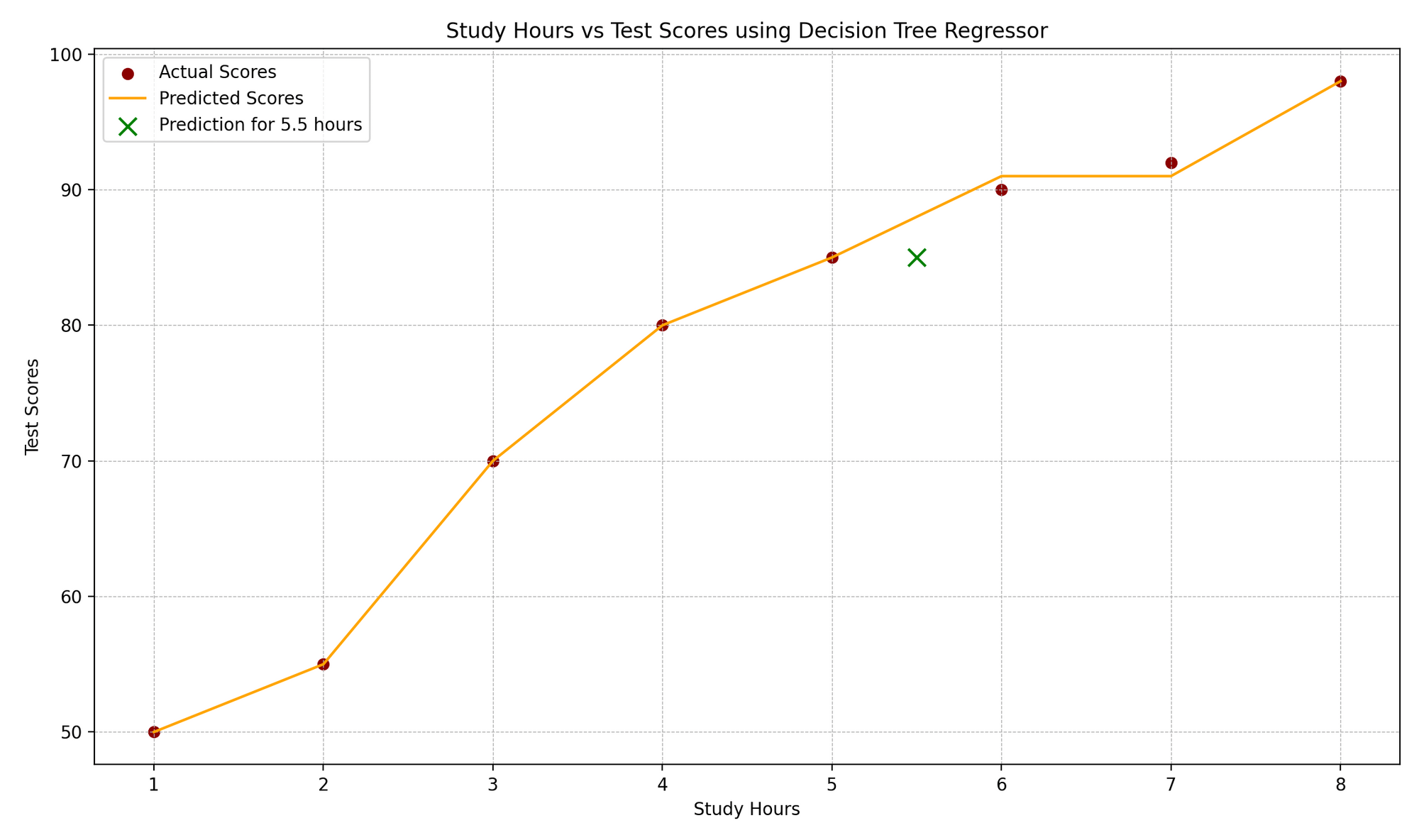
El gráfico “Horas de Estudio vs. Puntuaciones de los Exámenes” ilustra la correlación entre las horas de estudio y las puntuaciones correspondientes de los exámenes. Los puntos de datos reales se representan como puntos rojos, mientras que las predicciones del modelo se muestran como una función escalonada naranja, característica de los árboles de regresión. Un marcador “x” verde resalta una predicción para un nuevo punto de datos, que en este caso representa una duración de estudio de 5.5 horas. Los elementos de diseño del gráfico, como las líneas de cuadrícula, las etiquetas y las leyendas, mejoran la comprensión de los valores reales frente a los anticipados.

2.8 Bagging

Una de las mayores desventajas de los árboles de decisiones es su alta varianza. Podrías terminar con un modelo y predicciones que sean fáciles de explicar pero engañosas. Esto resultaría en conclusiones incorrectas y decisiones empresariales equivocadas.

Para reducir la varianza de los árboles de decisiones, se puede utilizar un método llamado Bagging. Para comprender qué es Bagging, hay dos términos que necesitas saber:

• Bootstrapping
• Teorema del límite central (CLT)

Puedes encontrar más información sobre el Bootstrapping, que es una técnica de remuestreo, más adelante en este manual. Por ahora, puedes pensar en el Bootstrapping como una técnica que realiza muestreo de los datos originales con reemplazo, lo que crea una copia de los datos muy similar pero no exactamente igual a los datos originales.

El Bagging también se basa en las mismas ideas que el CLT, que es uno de los teoremas más importantes, si no el más importante, en Estadística. Puedes leer más detalles sobre el CLT aquí.

Pero la idea que también se utiliza en el Bagging es que si tomas el promedio de muchas muestras, entonces la varianza se reduce significativamente en comparación con la varianza de cada uno de los modelos basados en muestras individuales.

Entonces, dado un conjunto de observaciones independientes Z1,…,Zn, cada una con una varianza σ2, la varianza de la media Z ̄ de las observaciones se calcula comoσ2/n. Por lo tanto, el promedio de un conjunto de observaciones reduce la varianza.

Para obtener más detalles estadísticos, consulta el siguiente tutorial:

Fundamentos De Estadística Para Científicos De Datos y Analistas De Datos Como Karl Pearson, un matemático británico ha afirmado, la estadística es la gramática de la ciencia y esto es especialmente válido para las Ciencias de la Computación y la Información, las Ciencias Físicas y las…Tatev Karen AslanyanLunarTech

El Bagging es básicamente una combinación de Bootstrap que construye árboles B utilizando muestras Bootstrap. El Bagging se puede utilizar para mejorar la precisión (reducir la varianza de muchos enfoques) tomando muestras repetidas de un solo conjunto de datos de entrenamiento.

Entonces, en el Bagging, generamos B muestras de entrenamiento Bootstrap, en base a las cuales se construyen B árboles similares (árboles correlacionados) que se agregan para calcular las predicciones, tomando el promedio de estas predicciones para estas B muestras. Es importante destacar que cada árbol se construye en un conjunto de datos de bootstrap, independiente de los demás árboles.

Así que, en el caso del Bagging, en cada división del árbol se consideran todas las características p, lo que resulta en árboles similares ya que cada vez los predictores más fuertes están en la parte superior y los más débiles en la parte inferior, lo que hace que todos los árboles en la bolsa se vean bastante similares entre sí.

2.8.1 Bagging en Árboles de Regresión

Para aplicar el Bagging a los árboles de regresión, simplemente construimos B árboles de regresión utilizando conjuntos de entrenamiento bootstrap y promediamos las predicciones resultantes. Estos árboles se expanden en profundidad y no se podan. Por lo tanto, cada árbol individual tiene alta varianza pero baja sesgo. El promedio de estos B árboles reduce la varianza.

2.8.2 Bagging en Árboles de Clasificación

Para una observación de prueba dada, podemos registrar la clase predicha por cada uno de los B árboles y tomar una mayoría de votos: la predicción general es la clase mayoritaria más común entre las B predicciones.

2.8.3 Estimación de Error Out-of-Bag (OOB)

Cuando aplicamos Bagging a los árboles de decisión, ya no es necesario aplicar la Validación Cruzada para estimar la tasa de error en la prueba. En el Bagging, ajustamos repetidamente los árboles a muestras bootstrap, y en promedio solo se utiliza un 2/3 de estas observaciones. El otro 1/3 no se utiliza durante el proceso de entrenamiento. Estas se llaman observaciones Out-of-bag.

Entonces, en total, hay B/3 predicciones por cada observación i que no se utiliza en el entrenamiento. Podemos tomar el promedio de los valores de respuesta para estos casos (o la clase mayoritaria). Entonces, por observación, el error OOB y el promedio de estos forman la tasa de error en la prueba.

2.8.4 Bagging en Python

Conoce a Lucy, una entrenadora de fitness que está interesada en predecir la pérdida de peso de sus clientes en función de su ingesta diaria de calorías y la duración de sus entrenamientos. Lucy tiene datos de clientes anteriores, pero reconoce que las predicciones individuales pueden estar sujetas a errores. Utilicemos Bagging para crear un modelo de predicción más estable.

Técnicamente, predeciremos un resultado continuo (pérdida de peso) en función de dos variables independientes (ingesta diaria de calorías y duración del entrenamiento), utilizando Bagging para reducir la varianza en las predicciones.

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import BaggingRegressorfrom sklearn.tree import DecisionTreeRegressor, plot_tree  # Asegúrate de importar plot_treefrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import mean_squared_error# Datos de ejemploclients_data = np.array([[2000, 60], [2500, 45], [1800, 75], [2200, 50], [2100, 62], [2300, 70], [1900, 55], [2000, 65]])weight_loss = np.array([3, 2, 4, 3, 3.5, 4.5, 3.7, 4.2])# División de entrenamiento y pruebaX_train, X_test, y_train, y_test = train_test_split(clients_data, weight_loss, test_size=0.25, random_state=42)# Creando un modelo de Baggingbase_estimator = DecisionTreeRegressor(max_depth=4)model = BaggingRegressor(base_estimator=base_estimator, n_estimators=10, random_state=42)# Entrenando el modelomodel.fit(X_train, y_train)# Predicción y evaluacióny_pred = model.predict(X_test)mse = mean_squared_error(y_test, y_pred)# Mostrando la predicción y evaluaciónprint(f"Pérdida de peso real: {y_test}")print(f"Pérdida de peso predicha: {y_pred}")print(f"Error Cuadrado Medio: {mse:.2f}")# Visualizando uno de los estimadores base (si se desea)plt.figure(figsize=(12, 8))tree = model.estimators_[0]plt.title('Uno de los Árboles de Decisión Base del Bagging')plot_tree(tree, filled=True, rounded=True, feature_names=["Ingesta de Calorías", "Duración del Entrenamiento"])plt.show()

Pérdida de peso real: [2.  4.5]Pérdida de peso predicha: [3.1  3.96]Error Cuadrado Medio: 0.75

• Datos de muestra: clients_data contiene la ingesta diaria de calorías y la duración del entrenamiento, y weight_loss contiene la pérdida de peso correspondiente.
• División de entrenamiento y prueba: Dividimos los datos en conjuntos de entrenamiento y prueba para validar el rendimiento predictivo del modelo.
• Creación y entrenamiento del modelo: Instanciamos BaggingRegressor con DecisionTreeRegressor como estimador base y lo entrenamos usando .fit() con nuestros datos de entrenamiento.
• Predicción y evaluación: Predecimos la pérdida de peso para los datos de prueba, evaluando la calidad de la predicción con el Error Cuadrático Medio (MSE).
• Visualización de uno de los estimadores base: Opcionalmente, visualizamos un árbol del conjunto para entender los procesos de toma de decisiones individuales (teniendo en cuenta que un árbol individual puede no funcionar bien, pero colectivamente producen predicciones estables).

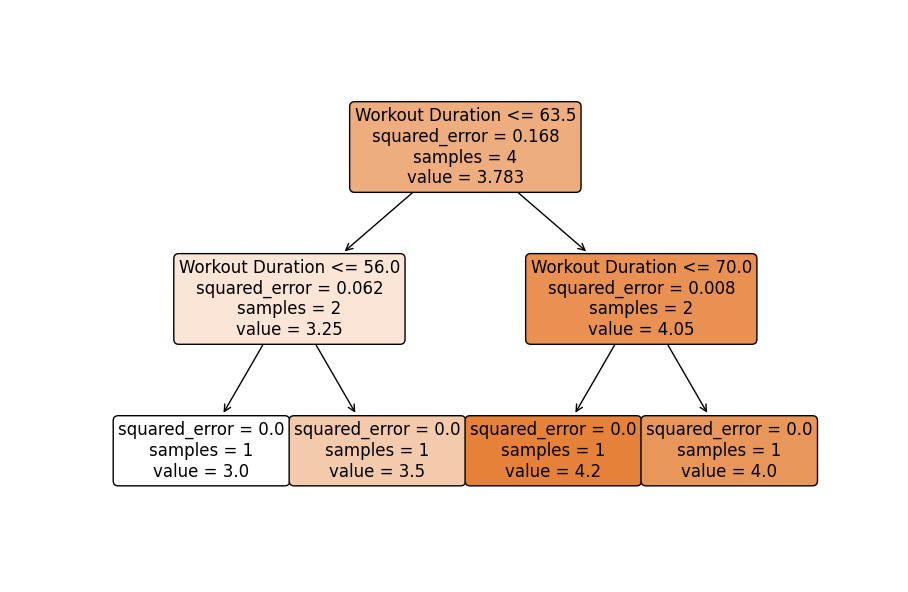
2.9 Random Forest

Los bosques aleatorios mejoran los árboles en conjunto a través de un pequeño ajuste que descorrelaciona los árboles.

Al igual que en el conjunto, construimos varios árboles de decisión en muestras de entrenamiento sacadas con reemplazo. Pero al construir estos árboles de decisión, cada vez que se considera una división en un árbol, se elige una muestra aleatoria de m predictores como candidatos de división entre el conjunto completo de p predictores.

La división solo puede usar uno de esos m predictores. Se toma una muestra nueva y aleatoria de m predictores en cada división, y típicamente elegimos m ≈ √p — es decir, el número de predictores considerados en cada división es aproximadamente igual a la raíz cuadrada del número total de predictores. Esta es también la razón por la que se llama Bosque Aleatorio “aleatorio”.

La diferencia principal entre el conjunto y los bosques aleatorios es que el tamaño del subconjunto de predictores m escogido por la descorrelación de los árboles.

Usar un valor pequeño de m al construir un bosque aleatorio suele ser útil cuando se tiene un gran número de predictores correlacionados. Entonces, si tienes un problema de Multicolinealidad, RF es un buen método para resolver ese problema.

Así que, a diferencia del conjunto, en el caso del Bosque Aleatorio, en cada división de árbol no se consideran todos los p predictores, sino solo m predictores seleccionados al azar de él. Esto resulta en árboles no similares que están descorrelacionados. Y debido a que el promedio de árboles descorrelacionados produce una menor varianza, el Bosque Aleatorio es más preciso que el conjunto.

2.9.1 Implementación de Random Forest en Python

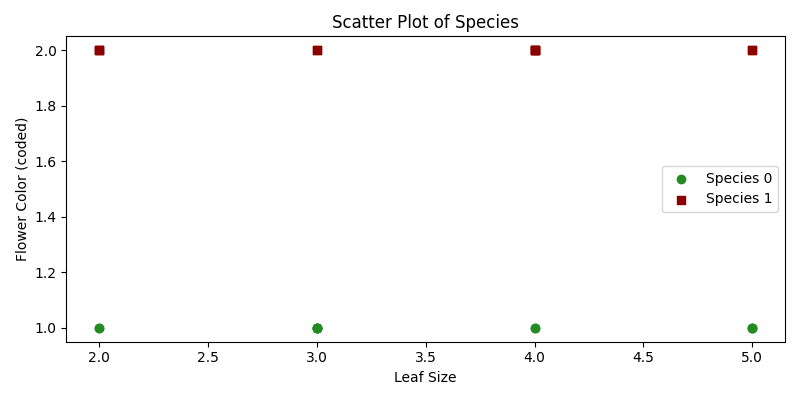
Noah es un botánico que ha recopilado datos sobre varias especies de plantas y sus características, como el tamaño de las hojas y el color de las flores. Noah está curioso si puede predecir la especie de una planta en función de estas características.

Aquí, utilizaremos el Bosque Aleatorio, un método de aprendizaje en conjunto, para ayudarlo a clasificar plantas.

Técnicamente, nuestro objetivo es clasificar especies de plantas en función de ciertas variables predictoras utilizando un modelo de Bosque Aleatorio.

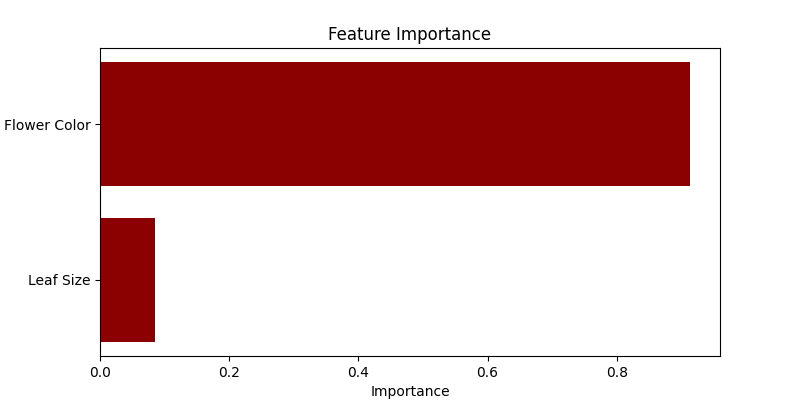
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import classification_report# Datos Expandidosplants_features = np.array([    [3, 1], [2, 2], [4, 1], [3, 2], [5, 1], [2, 2], [4, 1], [5, 2],    [3, 1], [4, 2], [5, 1], [3, 2], [2, 1], [4, 2], [3, 1], [4, 2],    [5, 1], [2, 2], [3, 1], [4, 2], [2, 1], [5, 2], [3, 1], [4, 2]])plants_species = np.array([    0, 1, 0, 1, 0, 1, 0, 1,    0, 1, 0, 1, 0, 1, 0, 1,    0, 1, 0, 1, 0, 1, 0, 1])# División de entrenamiento y pruebaX_train, X_test, y_train, y_test = train_test_split(plants_features, plants_species, test_size=0.25, random_state=42)# Creación de un modelo de Bosque Aleatoriomodel = RandomForestClassifier(n_estimators=10, random_state=42)# Entrenamiento del Modeloodel.fit(X_train, y_train)# Predicción y Evaluacióny_pred = model.predict(X_test)classification_rep = classification_report(y_test, y_pred)# Mostrando Predicción y Evaluaciónprint("Informe de clasificación:")print(classification_rep)# Gráfico de dispersión que visualiza las Clasesplt.figure(figsize=(8, 4))for species, marker, color in zip([0, 1], ['o', 's'], ['forestgreen', 'darkred']):    plt.scatter(plants_features[plants_species == species, 0],                plants_features[plants_species == species, 1],                marker=marker, color=color, label=f'Especie {species}')plt.xlabel('Tamaño de hoja')plt.ylabel('Color de flor (codificado)')plt.title('Gráfico de dispersión de especies')plt.legend()plt.tight_layout()plt.show()# Visualización de la Importancia de las Característicasplt.figure(figsize=(8, 4))features_importance = model.feature_importances_features = ["Tamaño de hoja", "Color de flor"]plt.barh(features, features_importance, color = "darkred")plt.xlabel('Importancia')plt.ylabel('Característica')plt.title('Importancia de las Características')plt.show()

• Datos de muestra: plants_features contiene el tamaño de las hojas y el color de las flores, mientras que plants_species indica las especies de la planta respectiva.
• División de entrenamiento y prueba: Separamos los datos en conjuntos de entrenamiento y prueba.
• Creación y entrenamiento del modelo: Instanciamos RandomForestClassifier con un número especificado de árboles (10 en este caso) y lo entrenamos utilizando .fit() con nuestros datos de entrenamiento.
• Predicción y evaluación: Predecimos las especies para los datos de prueba y evaluamos las predicciones utilizando un informe de clasificación que proporciona precisión, recuperación, puntuación f1 y soporte.
• Visualización de la importancia de las características: Utilizamos un gráfico de barras horizontales para mostrar la importancia de cada característica en la predicción de la especie de la planta. Random Forest cuantifica la utilidad de las características durante el proceso de construcción del árbol, que visualizamos aquí.

‌2.10 Modelos de refuerzo o conjunto

Al igual que Bagging (promediando árboles de decisión correlacionados) y Random Forest (promediando árboles de decisión no correlacionados), el refuerzo tiene como objetivo mejorar las predicciones resultantes de un árbol de decisión. El refuerzo es un modelo supervisado de aprendizaje automático que se puede utilizar tanto para problemas de regresión como de clasificación.

A diferencia de Bagging o Random Forest, donde los árboles se construyen de forma independiente entre sí utilizando una de las B muestras bootstrap (copia del conjunto de datos de entrenamiento inicial), en el refuerzo, los árboles se construyen de forma secuencial y dependen entre sí. Cada árbol se construye utilizando información de los árboles previamente construidos.

El refuerzo no implica muestreo bootstrap. En su lugar, cada árbol se ajusta a una versión modificada del conjunto de datos original. Es un método para convertir aprendices débiles en aprendices fuertes.

En el refuerzo, cada nuevo árbol es un ajuste en una versión modificada del conjunto de datos original. Entonces, a diferencia de ajustar un solo árbol de decisión grande a los datos, lo que implica un ajuste fuerte de los datos y potencialmente un sobreajuste, el enfoque de refuerzo aprende lentamente.

Dado el modelo actual, ajustamos un árbol de decisión a los residuos del modelo. Es decir, ajustamos un árbol utilizando los residuos actuales, en lugar del resultado Y, como respuesta. Luego agregamos este nuevo árbol de decisión a la función ajustada para actualizar los residuos.

Cada uno de estos árboles puede ser bastante pequeño, con solo algunos nodos terminales, determinados por el parámetro d en el algoritmo. Ahora echemos un vistazo a los 3 modelos de refuerzo más populares en el aprendizaje automático:

• AdaBoost
• GBM
• XGBoost

2.10.1 Refuerzo: AdaBoost

El primer algoritmo de conjunto en el que nos fijaremos hoy es AdaBoost. Al igual que en todas las técnicas de refuerzo, en el caso de AdaBoost los árboles se construyen utilizando la información del árbol anterior, y más específicamente, parte del árbol que no funcionó bien. Esto se llama aprendiz débil (Stump de decisión). Este Stump de decisión se construye utilizando solo un predictor y no todos los predictores para realizar la predicción.

Entonces, AdaBoost combina aprendices débiles para hacer clasificaciones y cada stump se hace utilizando los errores del stump anterior. Aquí tienes el plan paso a paso para construir un modelo AdaBoost:

• Paso 1: Asignación de pesos iniciales: asignar un peso igual a todas las observaciones en la muestra, donde este peso representa la importancia de que las observaciones se clasifiquen correctamente: 1/N (todas las muestras son igualmente importantes en esta etapa).
• Paso 2: Selección del predictor óptimo: se construye el primer stump obteniendo el RSS (en caso de regresión) o el índice de GINI/Entropía (en caso de clasificación) para cada predictor. Se selecciona el stump que hace el mejor trabajo en términos de precisión de predicción: el stump con el menor RSS o GINI/Entropía se selecciona como el siguiente árbol.
• Paso 3: Cálculo del peso de los Stumps según el error total de los stumps: se determina entonces la importancia de este stump en el árbol final utilizando el error total que este stump está cometiendo. Donde un stump que no es mejor que un lanzamiento aleatorio de una moneda con un error total igual a 0.5 obtiene un peso de 0. Peso = 0.5*log(1-Error total/Error total)
• Paso 4: Actualización de los pesos de las observaciones: aumentamos el peso de las observaciones que han sido predichas incorrectamente y disminuimos las observaciones restantes que tenían una mayor precisión o que se han clasificado correctamente, para que el próximo stump tenga una mayor importancia al predecir correctamente el valor de esta observación.
• Paso 5: Construcción del siguiente stump en función de los pesos actualizados: Uso del índice Gini ponderado para elegir el siguiente stump.
• Paso 6: Combinación de los B stumps: luego, todos los stumps se combinan teniendo en cuenta su importancia, suma ponderada.

Implementación de AdaBoost en Python

Imagina un escenario en el que queremos predecir los precios de las casas en función de ciertas características, como el número de habitaciones y la edad de la casa.

Para este ejemplo, generemos datos sintéticos donde: num_rooms: El número de habitaciones en la casa. house_age: La edad de la casa en años. price: El precio de la casa en miles de dólares:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import mean_squared_error

# Semilla para reproducibilidad
np.random.seed(42)

# Generar datos sintéticos
num_samples = 200
num_rooms = np.random.randint(3, 10, num_samples)
house_age = np.random.randint(1, 100, num_samples)
noise = np.random.normal(0, 50, num_samples)

# Supongamos una relación lineal con price = 50*rooms + 0.5*age + noise
price = 50*num_rooms + 0.5*house_age + noise

# Crear DataFrame
data = pd.DataFrame({'num_rooms': num_rooms, 'house_age': house_age, 'price': price})

# Graficar
plt.scatter(data['num_rooms'], data['price'], label='Num Rooms vs Price', color = 'forestgreen')
plt.scatter(data['house_age'], data['price'], label='House Age vs Price', color = 'darkred')
plt.xlabel('Valor de la Característica')
plt.ylabel('Precio')
plt.legend()
plt.title('Gráficos de Dispersión de Características vs Precio')
plt.show()

# Dividir los datos en conjuntos de entrenamiento y prueba
X = data[['num_rooms', 'house_age']]
y = data['price']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Iniciar y entrenar modelo AdaBoost Regressor
model_ab = AdaBoostRegressor(n_estimators=100, random_state=42)
model_ab.fit(X_train, y_train)

# Predecir
predictions = model_ab.predict(X_test)

# Evaluar el modelo
mse = mean_squared_error(y_test, predictions)
rmse = np.sqrt(mse)
print(f"Error Cuadrático Medio: {mse:.2f}")
print(f"Raíz del Error Cuadrático Medio: {rmse:.2f}")

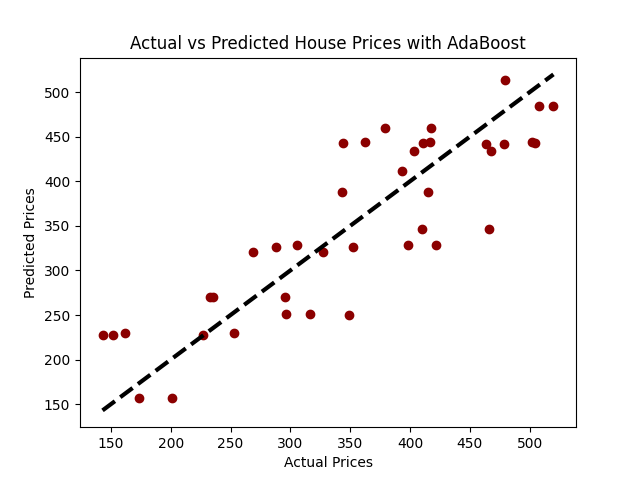
# Visualización: Precios Reales vs Precios Predichos
plt.scatter(y_test, predictions, color = 'darkred')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)
plt.xlabel('Precios Reales')
plt.ylabel('Precios Predichos')
plt.title('Precios Reales vs Precios Predichos con AdaBoost')
plt.show()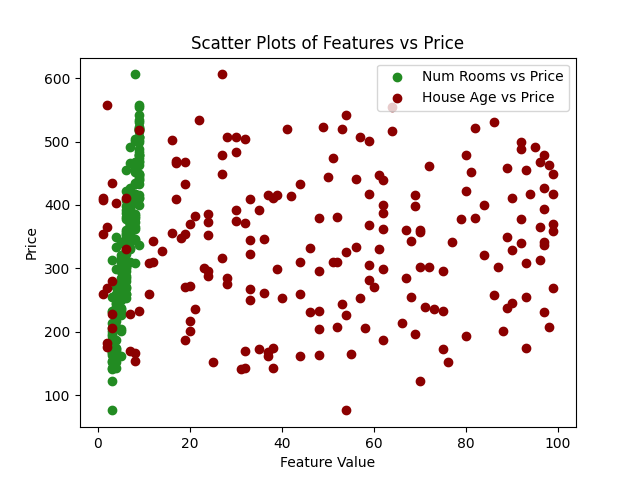

2.10.2 Algoritmo de Boosting: Modelo de Gradient Boosting (GBM)

AdaBoost y Gradient Boosting son muy similares entre sí. Pero en comparación con AdaBoost, que comienza el proceso seleccionando un tronco y continuando construyéndolo utilizando los aprendices débiles del tronco anterior, Gradient Boosting comienza con una sola hoja en lugar de un árbol o tronco.

El resultado correspondiente a esta hoja elegida es entonces una suposición inicial para la variable de resultado. Al igual que en el caso de AdaBoost, Gradient Boosting utiliza los errores del tronco anterior para construir el árbol. Pero a diferencia de AdaBoost, los árboles que Gradient Boosting construye son más grandes que un tronco. Eso es un parámetro donde establecemos un número máximo de hojas.

Para asegurarse de que el árbol no esté sobreajustando, Gradient Boosting utiliza la Tasa de Aprendizaje para escalar las contribuciones del gradiente. Gradient Boosting se basa en la idea de que dar muchos pasos pequeños en la dirección correcta (gradientes) dará como resultado una menor varianza (para datos de prueba).

La diferencia principal entre los algoritmos AdaBoost y Gradient Boosting es cómo tienen en cuenta las deficiencias de los aprendices débiles (por ejemplo, árboles de decisión). Mientras que el modelo AdaBoost identifica las deficiencias utilizando puntos de datos con un peso alto, el gradient boosting lo hace utilizando gradientes en la función de pérdida (y=ax+b+e, e necesita una mención especial ya que es el término de error).

La función de pérdida es una medida que indica qué tan buenos son los coeficientes de un modelo para ajustarse a los datos subyacentes. La comprensión lógica de la función de pérdida dependerá de lo que estemos tratando de optimizar.

Detención Temprana

El proceso especial de ajuste del número de iteraciones para un algoritmo (como GBM y Random Forest) se llama “Early Stopping” – un fenómeno que mencionamos cuando hablamos sobre los Árboles de Decisión.

Early Stopping realiza la optimización del modelo monitoreando el rendimiento del modelo en un conjunto de datos de prueba separado y deteniendo el procedimiento de entrenamiento una vez que el rendimiento en los datos de prueba deja de mejorar más allá de cierto número de iteraciones.

Evita el sobreajuste al intentar seleccionar automáticamente el punto de inflexión donde el rendimiento en el conjunto de datos de prueba comienza a disminuir mientras que el rendimiento en el conjunto de datos de entrenamiento continúa mejorando a medida que el modelo comienza a sobreajustarse.

En el contexto de GBM, el early stopping puede basarse en un conjunto de muestra fuera de bolsa (“OOB”) o en validación cruzada (“CV”). Como se mencionó anteriormente, el momento ideal para detener el entrenamiento del modelo es cuando el error de validación ha disminuido y comenzado a estabilizarse antes de que comience a aumentar debido al sobreajuste.

Para construir GBM, sigue este proceso paso a paso:

• Paso 1: Entrena el modelo en los datos existentes para predecir la variable objetivo
• Paso 2: Calcula la tasa de error utilizando las predicciones y los valores reales (Pseudo Residual)
• Paso 3: Utiliza las características existentes y el Pseudo Residual como variable objetivo para predecir los residuos nuevamente
• Paso 4: Utiliza los residuos predichos para actualizar las predicciones del Paso 1, escalando esta contribución al árbol con una tasa de aprendizaje (hiperparámetro)
• Paso 5: Repite los pasos 1-4, el proceso de actualización de los pseudo residuos y el árbol mientras se escala con la tasa de aprendizaje, para moverse lentamente en la dirección correcta hasta que ya no haya una mejora o lleguemos a nuestra regla de detención

La idea es que cada vez que agregamos un nuevo árbol escalado al modelo, los residuos deberían ser más pequeños.

En cualquier paso m, el modelo de Boosting de Gradiente produce un modelo que es un conjunto del paso anterior F(m-1) y la tasa de aprendizaje eta multiplicada por la derivada negativa de la función de pérdida con respecto a la salida del modelo en el paso m-1: (weak learner en el paso m-1).

Implementación de GBM en Python

# Inicializar y entrenar el modelo Gradient Boosting Regressormodel_gbm = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=1, random_state=42)model_gbm.fit(X_train, y_train)# Prediccionespredictions = model_gbm.predict(X_test)# Evaluar el modelomse = mean_squared_error(y_test, predictions)rmse = np.sqrt(mse)print(f"Error Cuadrado Medio: {mse:.2f}")print(f"Error Cuadrado Medio Raíz: {rmse:.2f}")# Visualización: Precios Reales vs Precios Predichosplt.scatter(y_test, predictions, color = 'orange')plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)plt.xlabel('Precios Reales')plt.ylabel('Precios Predichos')plt.title('Precios Reales vs Precios Predichos con GBM')plt.show()

‌                                              

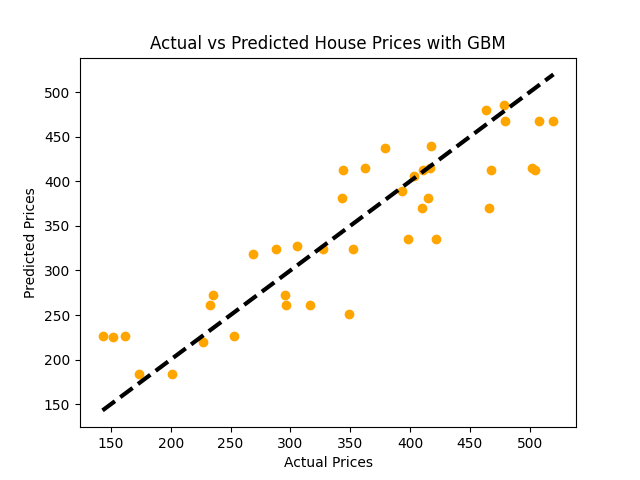
2.10.3 Algoritmo de Boosting: XGBoost

Uno de los algoritmos de Boosting o de Ensemble más populares es Extreme Gradient Boosting (XGBoost).

La diferencia entre GBM y XGBoost es que en el caso de XGBoost se calculan las derivadas de segundo orden (gradientes de segundo orden). Esto proporciona más información sobre la dirección de los gradientes y cómo llegar al mínimo de la función de pérdida.

Recuerda que esto es necesario para identificar el weak learner y mejorar el modelo mejorando los weak learners.

La idea detrás de XGBoost es que la segunda derivada tiende a ser más precisa en términos de encontrar la dirección precisa. Al igual que AdaBoost, XGBoost aplica una regularización avanzada en forma de normas L1 o L2 para abordar el sobreajuste.

A diferencia de AdaBoost, XGBoost es paralelizable debido a su mecanismo especial de almacenamiento en caché, lo que lo hace conveniente para manejar conjuntos de datos grandes y complejos. Además, para acelerar el entrenamiento, XGBoost utiliza un Algoritmo Avaricioso Aproximado para considerar solo una cantidad limitada de umbrales para dividir los nodos de los árboles.

Para construir un modelo XGBoost, sigue este proceso paso a paso:

• Paso 1: Ajusta un solo árbol de decisión: En este paso, se calcula la función de pérdida, por ejemplo, NDCG, para evaluar el modelo.
• Paso 2: Agrega el segundo árbol: Se hace de manera que cuando se agrega este segundo árbol al modelo, disminuye la función de pérdida basada en las derivadas de primer y segundo orden en comparación con el árbol anterior (donde también se usó la tasa de aprendizaje eta).
• Paso 3: Encontrar la dirección del próximo movimiento: Usando las derivadas de primer y segundo grado, podemos encontrar la dirección en la cual la función de pérdida disminuye más. Básicamente, es el gradiente de la función de pérdida con respecto a la salida del modelo anterior.
• Paso 4: Dividir los nodos: Para dividir las observaciones, XGBoost utiliza el algoritmo aproximado Avaricioso (por lo general, alrededor de 3 cuantiles ponderados aproximados) que tienen una suma similar de pesos. Para encontrar el valor de división de los nodos, no considera todos los umbrales candidatos, sino que solo utiliza los cuantiles de ese predictor.

La tasa de aprendizaje óptima se puede determinar utilizando la Validación Cruzada y la Búsqueda en Rejilla.

Implementación simple de XGBoost en Python

Imagina que tienes un conjunto de datos que contiene información sobre varias casas y sus precios. El conjunto de datos incluye características como el número de habitaciones, baños, el área total, el año de construcción, entre otras, y quieres predecir el precio de una casa basado en estas características.

import xgboost as xgb# Inicializa y entrena el modelo XGBoostmodel_xgb = xgb.XGBRegressor(objective ='reg:squarederror', n_estimators = 100, seed = 42)model_xgb.fit(X_train, y_train)# Prediccionespredictions = model_xgb.predict(X_test)# Evaluar el modelomse = mean_squared_error(y_test, predictions)rmse = np.sqrt(mse)print(f"Error Cuadrado Medio: {mse:.2f}")print(f"Error Cuadrado Medio Raíz: {rmse:.2f}")# Visualización: Precios Reales vs Precios Predichosplt.scatter(y_test, predictions, color="forestgreen")plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)plt.xlabel('Precios Reales')plt.ylabel('Precios Predichos')plt.title('Precios de Casas Reales vs. Predichos con XGBoost')plt.show()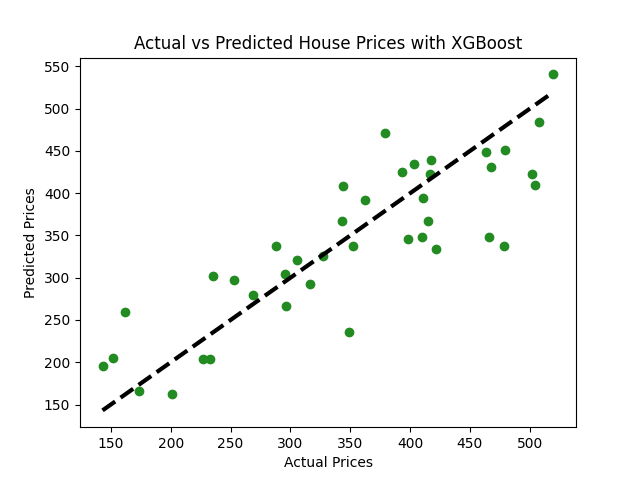

Capítulo 3: Selección de Características en Aprendizaje Automático

La ruta hacia la construcción de modelos de aprendizaje automático efectivos a menudo involucra una pregunta crítica: ¿qué características debemos incluir para generar predicciones confiables al mismo tiempo que mantenemos el modelo simple e comprensible? Aquí es donde la selección de subconjuntos juega un papel clave.

En Aprendizaje Automático, en muchos casos estamos lidiando con una gran cantidad de características y no todas ellas suelen ser importantes e informativas para el modelo. Incluir variables irrelevantes en el modelo conduce a una complejidad innecesaria en el modelo de Aprendizaje Automático y afecta tanto su interpretabilidad como su rendimiento.

Al eliminar estas variables no importantes y seleccionar solo características relativamente informativas, podemos obtener un modelo que sea más fácil de interpretar y posiblemente más preciso.

Veamos un ejemplo específico de un modelo de Aprendizaje Automático para simplificar las cosas.

Supongamos que estamos analizando un modelo de Regresión Lineal Múltiple (múltiples variables independientes y una variable de respuesta/dependiente) con un número muy grande de características. Este modelo probablemente sea complejo en cuanto a su interpretación. Además, puede resultar en predicciones inexactas ya que algunas de esas características pueden ser irrelevantes y no ayudan a explicar la variable de respuesta.

El proceso de selección de variables importantes en el modelo se llama selección de características o selección de variables. Este proceso implica identificar un subconjunto de las p variables que creemos están relacionadas con la variable dependiente o de respuesta. Para ello, es necesario ejecutar la regresión para todas las combinaciones posibles de variables independientes y seleccionar aquella que resulte en el modelo de mejor rendimiento o el peor rendimiento.

Existen varias aproximaciones que puedes usar para la selección de características, generalmente divididas en las siguientes 3 categorías:

• Selección de subconjuntos (Mejor selección de subconjunto, Selección de características paso a paso)
• Técnicas de regularización (Regresiones L1 Lasso, L2 Ridge)
• Técnicas de reducción de dimensionalidad (PCA)

3.1 Selección de subconjuntos en Machine Learning

La selección de subconjuntos en machine learning es una técnica diseñada para identificar y utilizar un subconjunto de características importantes, mientras se omiten las demás. Esto ayuda a crear modelos más fáciles de interpretar y, en algunos casos, predecir con mayor precisión al evitar el sobreajuste.

Al navegar entre numerosas características, se vuelve vital elegir selectivamente aquellas que impactan significativamente al modelo predictivo. La selección de subconjuntos proporciona un enfoque sistemático para examinar posibles combinaciones de predictores. Su objetivo es seleccionar un subconjunto que represente de manera efectiva los datos sin una complejidad innecesaria.

• Mejor selección de subconjunto: Examina todas las combinaciones posibles y selecciona el conjunto de predictores más óptimo.
• Selección paso a paso: Agrega o elimina predictores incrementalmente, lo cual incluye selección hacia adelante y hacia atrás.
• Selección de subconjuntos aleatoria: Escoge subconjuntos al azar, introduciendo un elemento de aleatoriedad en la selección del modelo.

Es un equilibrio entre utilizar todos los predictores disponibles, arriesgando la sobrecomplejidad y el posible sobreajuste del modelo, y construir un modelo demasiado simple que pueda pasar por alto patrones de datos importantes.

En esta sección, exploraremos estas técnicas de selección de subconjuntos. Aprenderás cómo funciona cada enfoque y cómo afecta el rendimiento del modelo, asegurando que los modelos que construyamos sean confiables, simples y efectivos.

3.1.1 Técnicas de selección de características paso a paso

Una de las técnicas populares de selección de subconjuntos es la técnica de selección de características paso a paso. Veamos dos métodos diferentes de selección de características paso a paso:

• Selección hacia adelante paso a paso
• Selección hacia atrás paso a paso

Selección hacia adelante paso a paso: Lo que hace esta técnica es comenzar con un modelo nulo vacío con solo una intersección. Luego ejecutamos una serie de regresiones simples y elegimos la variable que tiene un modelo con la RSS (Suma de Cuadrados Residuales) más pequeña. Luego hacemos lo mismo con regresiones de 2 variables y continuamos hasta que se complete.

Entonces, la selección hacia adelante paso a paso comienza con un modelo que no contiene predictores y luego agrega predictores al modelo, uno a la vez, hasta que todos los predictores estén en el modelo. En particular, en cada paso se agrega al modelo la variable que proporciona la mayor mejora adicional al ajuste.

La selección hacia adelante paso a paso se puede resumir de la siguiente manera:

Paso 1: Sea M_0 el modelo nulo, que no contiene características.

Paso 2: Para K = 0,…, p-1:

• Considera todos los (p-k) modelos que contienen las variables en M_k con una característica adicional o predictor.
• Elige el mejor modelo entre estos p-k modelos y defínelo como M_(k+1) utilizando métricas de rendimiento como RSS/R-cuadrado.

Paso 3: Selecciona el modelo único con el mejor rendimiento entre estos modelos M_0,…,M_p (el que tenga el menor error de validación cruzada, C_p, AIC (Criterio de Información de Akaike), BIC (Criterio de Información Bayesiano) o R-cuadrado ajustado es tu mejor modelo M*).

Entonces, la idea detrás de esta selección es comenzar de manera simple y aumentar el número de predictores en el modelo. Por número de predictores, considera todas las posibles combinaciones de variables y selecciona un solo mejor modelo: M_k. Luego, compara todos estos modelos con diferentes números de predictores (mejores M_ks) y selecciona el que tenga el mejor rendimiento.

Cuando n < p, es decir, cuando el número de observaciones es mayor que el número de predictores en la regresión lineal, puedes usar este enfoque para seleccionar características en el modelo para que la regresión lineal funcione en primer lugar.

Selección hacia atrás paso a paso: A diferencia de la selección hacia adelante paso a paso, en el caso de la selección hacia atrás paso a paso, el algoritmo de selección de características comienza con el modelo completo que contiene todos los p predictores. Luego se selecciona el mejor modelo con p predictores.

En consecuencia, el modelo elimina de a uno las variables con el valor p más alto y nuevamente se selecciona el mejor modelo.

Cada vez, el modelo se ajusta nuevamente para identificar la variable menos estadísticamente significativa hasta que se cumpla la regla de detención. (Por ejemplo, todos los valores p deben ser menores que el 5%.) Luego, comparamos todos estos modelos con diferentes números de predictores (mejores M_ks) y seleccionamos el modelo único con el mejor rendimiento entre estos modelos M_0,….M_p (el que tenga el Error de Validación Cruzada, C_p, AIC (Criterio de Información de Akaike), BIC (Criterio de Información Bayesiana) o R-cuadrado ajustado más pequeño es tu mejor modelo M*).

La selección de características hacia atrás paso a paso se puede resumir de la siguiente manera:

Paso 1: Sea M_p el modelo completo, que contiene todas las características.

Paso 2: Para k= p, p-1 ….,1:

• Considere todos los k modelos que contienen todas las variables excepto una de las predictoras en el modelo M_k, para k – 1 características.
• Elija el mejor modelo entre estos k modelos y defínalo como M_(k-1) utilizando métricas de rendimiento como RSS/R-cuadrado.

Paso 3: Seleccione el modelo único con el mejor rendimiento entre estos modelos M_0,….M_p (el que tenga el Error de Validación Cruzada, C_p, AIC (Criterio de Información de Akaike), BIC (Criterio de Información Bayesiana) o R-cuadrado ajustado más pequeño es tu mejor modelo M*).

Al igual que la selección hacia adelante paso a paso, la técnica de selección de características hacia atrás paso a paso busca solo a través de (p+1)/2 modelos, lo que la hace posible de aplicar en entornos donde p es demasiado grande para aplicar otras técnicas de selección.

Además, no se garantiza que la selección de características hacia atrás paso a paso genere el mejor modelo que contenga un subconjunto de los p predictores. Se requiere que el número de observaciones o puntos de datos n sea mayor que el número de variables del modelo p, mientras que la selección hacia adelante paso a paso se puede utilizar incluso cuando n < p.

3.2 Regularización en el Aprendizaje Automático

La regularización, también conocida como contracción, es una estrategia ampliamente utilizada para abordar el problema del sobreajuste en modelos de aprendizaje automático.

El concepto fundamental de la regularización implica introducir deliberadamente un ligero sesgo en el modelo, con el beneficio de reducir notablemente su variabilidad.

El término “contracción” se deriva de la capacidad del método de hacer que algunos de los coeficientes estimados tiendan a cero, imponiendo una penalización sobre ellos para evitar que eleven en exceso la varianza del modelo.

Dos técnicas de regularización prominentes se destacan en la práctica: la regresión Ridge, que utiliza la norma L2, y la regresión Lasso, que utiliza la norma L1.

3.2.1 Regresión Ridge (Regularización L2)

Examinemos ejemplos de regresión lineal múltiple, en los que pp variables independientes o predictores se utilizan para modelar la variable dependiente yy.

Vale la pena recordar que el Método de los Mínimos Cuadrados Ordinarios (OLS), siempre y cuando se cumplan sus suposiciones, es una técnica de estimación ampliamente adoptada para determinar los parámetros de la regresión lineal. OLS busca los coeficientes óptimos minimizando la suma residual de cuadrados (RSS) del modelo. Esto es:

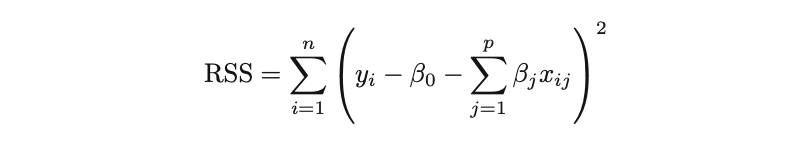
donde β representa las estimaciones de los coeficientes para diferentes variables o predictores (X).

La regresión Ridge es bastante similar a OLS, excepto que los coeficientes se estiman minimizando una función de coste o pérdida ligeramente diferente. Es decir, las estimaciones de los coeficientes βˆR de la regresión de Ridge se minimizan mediante la siguiente función de pérdida:

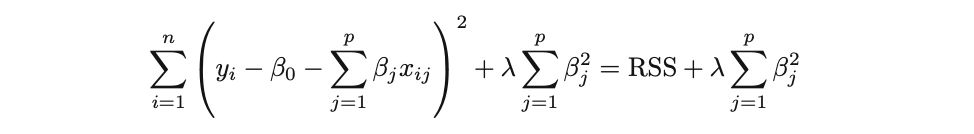
donde λ (lambda, que siempre es positivo, ≥ 0) es el parámetro de ajuste o el parámetro de penalización, y como se puede ver en esta fórmula, en el caso de Ridge, se utiliza la penalización L2 o la norma L2.

De esta manera, la regresión de Ridge asignará una penalización a algunas variables, reduciendo sus coeficientes hacia cero, lo cual disminuye la varianza general del modelo, pero estos coeficientes nunca se volverán exactamente cero. Por lo tanto, los parámetros del modelo nunca se establecen exactamente en 0, lo que significa que todos los p predictores del modelo siguen intactos.

Norma L2 (distancia euclidiana)

La norma L2 es un término matemático que proviene del álgebra lineal. Representa una norma euclidiana que se puede representar de la siguiente manera:

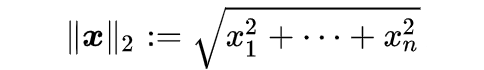
Parámetro de ajuste λ: el parámetro de ajuste λ sirve para controlar el impacto relativo de la penalización en las estimaciones de los coeficientes de regresión. Cuando λ = 0, el término de penalización no tiene efecto y la regresión de ridge producirá las estimaciones de mínimos cuadrados ordinarios. Pero a medida que λ → ∞ (se vuelve muy grande), el impacto de la penalización por reducción crece y las estimaciones de los coeficientes de regresión de la regresión de ridge se acercan a 0. Aquí hay una representación visual de esto:

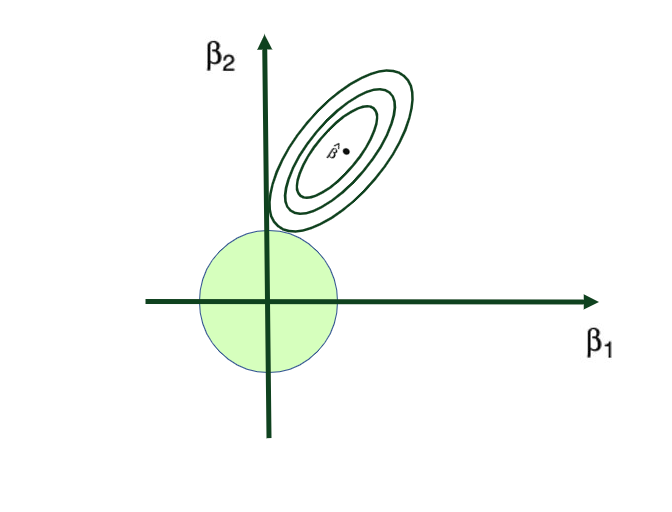
¿Por qué funciona la regresión de Ridge?

La ventaja de la regresión de Ridge sobre los mínimos cuadrados ordinarios proviene del fenómeno de compensación sesgo-varianza. A medida que λ, el parámetro de penalización, aumenta, la flexibilidad del ajuste de regresión de ridge disminuye, lo que conduce a una varianza reducida pero a un sesgo aumentado.

3.2.2 Regresion Lasso (Regularización L1)

La regresión Lasso supera esta desventaja de la regresión de Ridge. Es decir, las estimaciones de los coeficientes de regresión Lasso βˆλL son los valores que minimizan:

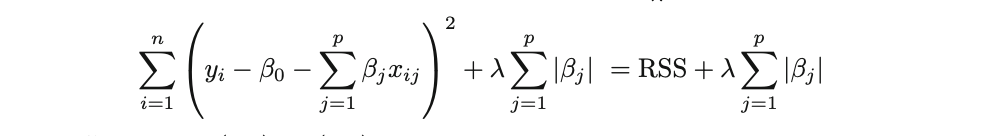
Al igual que con la regresión de Ridge, Lasso reduce las estimaciones de los coeficientes hacia cero. Pero en el caso de Lasso, se utiliza la penalización L1 o la norma L1, lo que tiene el efecto de forzar que algunas de las estimaciones de los coeficientes sean exactamente iguales a cero cuando el parámetro de ajuste λ es significativamente grande.

Entonces, al igual que muchas técnicas de selección de características, la regresión de Lasso realiza selección de variables además de resolver el problema de sobreajuste.

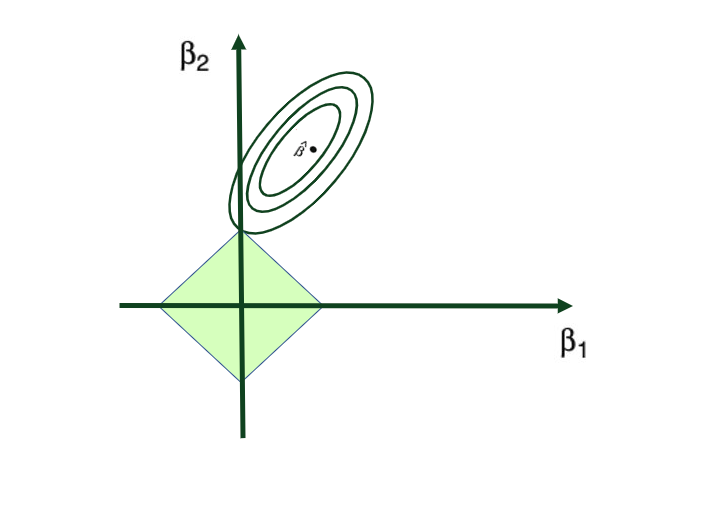
Norma L1 (distancia de Manhattan)

La norma L1 es un término matemático que proviene del álgebra lineal. Representa una norma de Manhattan que se puede representar de la siguiente manera:

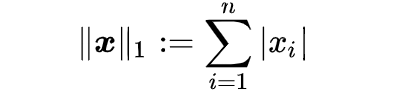
¿Por qué funciona la regresión de Lasso?

Al igual que con la regresión de Ridge, la ventaja de la regresión de Lasso sobre los mínimos cuadrados ordinarios proviene de la compensación sesgo-varianza introducida anteriormente. A medida que λ aumenta, la flexibilidad del ajuste de regresión de ridge disminuye, lo que conduce a una varianza reducida pero a un sesgo aumentado. Además, Lasso también realiza selección de características.

3.2.3 Regresión Lasso vs Ridge

La regresión Lasso reduce las estimaciones de los coeficientes hacia cero e incluso fuerza que algunos de estos coeficientes sean exactamente iguales a cero cuando el parámetro de ajuste λ es significativamente grande. Entonces, al igual que muchas técnicas de selección de características, la regresión Lasso realiza selección de variables además de resolver el problema de sobreajuste.

La comparación entre Ridge Regression (regresión de Ridge) y Lasso Regression (regresión de Lasso) se vuelve clara al poner los dos gráficos anteriores uno al lado del otro:

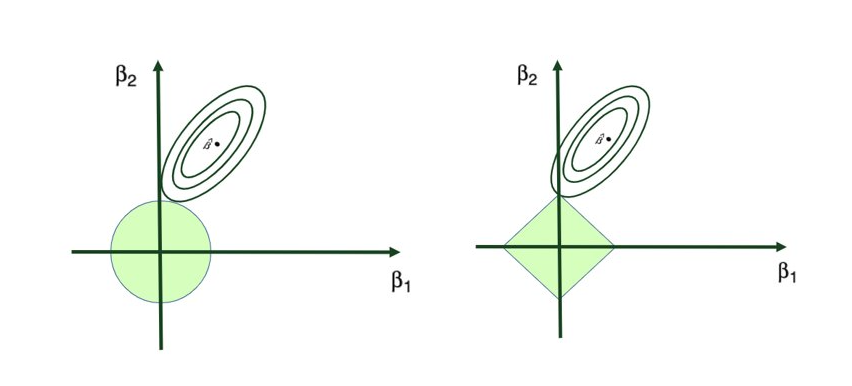
Si quieres aprender en detalle sobre la regularización, lee este tutorial:

Trade-Off de sesgo-varianza, sobreajuste y regularización en Machine LearningEl sobreajuste es un problema importante que forma parte esencial de la lista de verificación de modelado de cada científico de datos e ingeniero de aprendizaje automático. Entonces, si estás utilizando un enfoque estadístico, econométrico o…Tatev Karen AslanyanTowards Data Science

Capítulo 4: Técnicas de remuestreo en Machine Learning

Cuando solo tenemos datos de entrenamiento y queremos hacer juicios sobre el desempeño del modelo en datos no vistos, podemos usar técnicas de remuestreo para crear datos de prueba artificiales.

Las técnicas de remuestreo se dividen frecuentemente en dos categorías: validación cruzada y bootstrap. Se utilizan normalmente para los siguientes tres propósitos:

• Evaluación del modelo: evaluar el desempeño del modelo (para calcular la tasa de error de prueba)
• Varianza del modelo: calcular la varianza del modelo para verificar qué tan generalizable es tu modelo
• Selección del modelo: seleccionar la flexibilidad del modelo

Por ejemplo, para estimar la variabilidad de un ajuste de regresión lineal, podemos extraer muestras diferentes de los datos de entrenamiento repetidamente, ajustar una regresión lineal a cada muestra nueva y luego examinar en qué medida difieren los ajustes resultantes.

4.1 Validación cruzada

La validación cruzada se puede usar para estimar el error de prueba asociado a un método de aprendizaje estadístico dado con el fin de realizar:

• Evaluación del modelo: evaluar su desempeño calculando la tasa de error de prueba
• Selección del modelo: seleccionar el nivel adecuado de flexibilidad.

Se reserva un subconjunto de las observaciones de entrenamiento durante el proceso de ajuste y luego se aplica el método de aprendizaje estadístico a esas observaciones retenidas.

La validación cruzada generalmente se divide en las siguientes tres categorías:

• Enfoque de conjunto de validación
• Validación cruzada k-fold (Validación cruzada k-fold CV)
• Validación cruzada Leave One Out (LOOCV)

4.1.1 Enfoque de conjunto de validación

Este es un enfoque simple que divide los datos en conjuntos de entrenamiento y validación al azar. Este enfoque generalmente utiliza la función train_test_split() de Sklearn.

Luego, el modelo se entrena con los datos de entrenamiento (generalmente el 80% de los datos) y se utiliza para predecir los valores para el conjunto de validación o de prueba (generalmente el 20% de los datos), que es la tasa de error de prueba.

4.1.2 Validación cruzada Leave One Out (LOOCV)

LOOCV es similar al enfoque de conjunto de validación. Pero cada vez deja una observación fuera del conjunto de entrenamiento y utiliza las n-1 restantes para entrenar el modelo y calcular el ECM (error cuadrático medio) para esa predicción. Por lo tanto, en el caso de LOOCV, el modelo debe ser ajustado n veces (donde n es el número de observaciones en el modelo).

Luego, se repite este proceso para todas las observaciones y se calcula el ECM n veces. La media de los ECMs es la tasa de error de validación cruzada y se puede expresar de la siguiente manera:

‌        

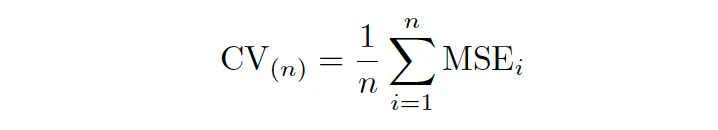
4.1.3 Validación cruzada k-fold (Validación cruzada k-fold CV)

CV de K-Fold es la solución perfecta entre el enfoque del conjunto de validación (alta varianza y sesgo alto pero computacionalmente eficiente) frente al LOOCV (sesgo bajo y varianza baja pero computacionalmente ineficiente).

En K-Fold CV, los datos se dividen aleatoriamente en K muestras del mismo tamaño (K-fold). Luego, cada vez se utiliza una como validación y el resto como entrenamiento, y el modelo se ajusta K veces. La media de los K errores cuadráticos medios forma la tasa de error de la prueba de validación cruzada.

Observe que el LOOCV es un caso especial de K-fold CV donde K = N, y puede expresarse de la siguiente manera:

‌                                            

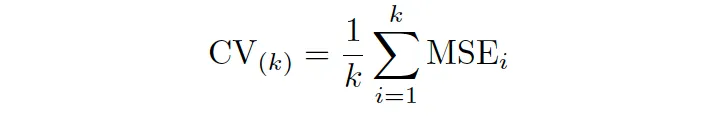
4.2 Selección del mejor K en K-Fold CV

La elección de k en K-Fold es una cuestión de compensación de sesgo-varianza y eficiencia del modelo. Por lo general, K-Fold CV y LOOCV proporcionan resultados similares y su rendimiento puede evaluarse utilizando datos simulados.

Sin embargo, LOOCV tiene un sesgo más bajo (insesgado) en comparación con K-fold CV porque LOOCV utiliza más datos de entrenamiento que K-fold CV. Pero LOOCV tiene una varianza más alta que K-fold porque LOOCV ajusta el modelo en datos casi idénticos para cada elemento y los resultados están altamente correlacionados en comparación con los resultados de K-Fold, que están menos correlacionados.

Dado que la media de resultados altamente correlacionados tiene una varianza más alta que la de resultados menos correlacionados, la varianza del LOOCV es mayor.

• K = N (LOOCV), cuanto mayor sea K → mayor varianza y menor sesgo
• K = 1, cuanto menor sea K → menor varianza y mayor sesgo

Teniendo en cuenta esta información, podemos calcular el rendimiento del modelo para varios K, por ejemplo, K = 3,5,6,7 …, 10 o el error de clasificación del modelo Tipo I, Tipo II y total en caso de un modelo de clasificación. Luego, el mejor modelo que tenga mejor rendimiento en K puede ser el K óptimo utilizando la idea de la curva ROC (caso de clasificación) o el método del Codo (caso de regresión).

4.3 Bootstrap

Bootstrap es otra técnica de remuestreo muy popular que se utiliza para diversos propósitos. Uno de ellos es estimar eficazmente la variabilidad de las estimaciones/modelos o crear muestras artificiales a partir de una muestra existente para mejorar el rendimiento del modelo (como en el caso de Bagging o Random Forest).

Se utiliza en muchas situaciones donde es difícil o incluso imposible calcular directamente la desviación estándar de una cantidad de interés.

• Es una forma muy útil de cuantificar la incertidumbre asociada con el método de aprendizaje estadístico y obtener los errores estándar/medida de variabilidad.
• No es útil para la Regresión Lineal, ya que el software estándar R/Python proporciona estos resultados (SE de los coeficientes).

Bootstrap es extremadamente útil para otros métodos donde es más difícil cuantificar la variabilidad. El muestreo por bootstrap se realiza con reemplazo, lo que significa que la misma observación puede ocurrir más de una vez en el conjunto de datos bootstrap.

Entonces, el Bootstrap toma la muestra de entrenamiento original y vuelve a muestrearla por reemplazo, lo que resulta en B muestras diferentes. Luego, para cada una de estas muestras simuladas, se calcula la estimación de los coeficientes. Luego, tomando la media de estas estimaciones de coeficientes y utilizando la fórmula común para el error estándar, calculamos el Error Estándar del modelo Bootstrap.

Lea más sobre esto aquí.‌                                              ‌             ‌

Capítulo 5: Técnicas de Optimización

Saber los fundamentos de los modelos de Aprendizaje Automático y aprender cómo entrenar esos modelos es definitivamente una gran parte para convertirse en un Científico de Datos técnico. Pero eso es solo una parte del trabajo.

Para utilizar el modelo de Aprendizaje Automático para resolver un problema empresarial, debe optimizarlo después de haber establecido su línea de base. Es decir, debe optimizar el conjunto de hiperparámetros en su modelo de Aprendizaje Automático para encontrar el conjunto de parámetros óptimos que resulten en el mejor modelo de rendimiento (suponiendo que todo lo demás sea igual).

Entonces, para optimizar o ajustar tu modelo de Machine Learning, necesitas realizar una optimización de hiperparámetros. Al encontrar la combinación óptima de valores de hiperparámetros, podemos disminuir los errores que produce el modelo y construir el modelo más preciso.

Un hiperparámetro del modelo es una constante en el modelo. Es externo al modelo, y su valor no puede estimarse a partir de los datos (sino que debe especificarse de antemano antes de entrenar el modelo). Por ejemplo, k en k-Nearest Neighbors (kNN) o el número de capas ocultas en las Redes Neuronales.

Los métodos de optimización de hiperparámetros generalmente se dividen en:

• Búsqueda Exhaustiva o Enfoque de Fuerza Bruta (como Búsqueda en Cuadrícula)
• Descenso de Gradiente (GD en Lote, SGD, SDG con Momentum, Adam)
• Algoritmos Genéticos

En este manual, solo hablaré sobre los dos primeros tipos de técnicas de optimización.

5.1 Enfoque de Fuerza Bruta (Búsqueda en Cuadrícula)

La búsqueda exhaustiva (también conocida como Búsqueda en Cuadrícula o Enfoque de Fuerza Bruta) es el proceso de buscar los hiperparámetros más óptimos revisando cada uno de los candidatos para los hiperparámetros y calculando la tasa de error del modelo.

Una vez que creamos la lista de valores posibles para cada uno de los hiperparámetros, para cada combinación posible de valores de hiperparámetros, calculamos la tasa de error del modelo y la comparamos con el modelo óptimo actual (aquel con la tasa de error mínima). Durante cada iteración, el modelo óptimo se actualiza si los nuevos valores de parámetros resultan en una tasa de error más baja.

El método de optimización es simple. Por ejemplo, si estás trabajando con un algoritmo de agrupamiento K-means, puedes buscar manualmente el número correcto de grupos. Pero si hay cientos o miles de combinaciones posibles de valores de hiperparámetros que debes considerar, el modelo puede tardar horas o días en entrenar, y se vuelve increíblemente pesado y lento. Por lo tanto, la búsqueda por fuerza bruta es ineficiente la mayor parte del tiempo.

Para optimizar o ajustar tu modelo de Machine Learning, necesitas realizar una optimización de hiperparámetros. Al encontrar la combinación óptima de valores de hiperparámetros, podemos disminuir el error que produce el modelo y construir el modelo más preciso.

Cuando se trata de técnicas de optimización del tipo Descenso de Gradiente, sus variantes como Descenso de Gradiente en Lote, Descenso de Gradiente Estocástico, y así sucesivamente difieren en términos de la cantidad de datos utilizados para calcular el gradiente de la función de pérdida o costo.

Definamos esta Función de Pérdida como J(θ) donde θ (theta) representa el parámetro que queremos optimizar.

La cantidad de uso de datos representa un equilibrio entre la precisión de la actualización del parámetro y el tiempo que lleva realizar dicha actualización. Es decir, cuanto mayor sea la muestra de datos que usemos, podemos esperar un ajuste más preciso de un parámetro, pero el proceso será mucho más lento.

Lo mismo ocurre a la inversa. Cuanto menor sea la muestra de datos, menos precisos serán los ajustes en el parámetro, pero el proceso será mucho más rápido.

5.2 Optimización por Descenso de Gradiente (GD)

El algoritmo de Descenso de Gradiente en Lote (a menudo llamado simplemente Descenso de Gradiente o GD) calcula el gradiente de la Función de Pérdida J(θ) con respecto al parámetro objetivo utilizando todos los datos de entrenamiento.

Hacemos esto primero prediciendo los valores para todas las observaciones en cada iteración y comparándolos con el valor dado en los datos de entrenamiento. Estos dos valores se utilizan para calcular el término de error de predicción por observación, que luego se utiliza para actualizar los parámetros del modelo. Este proceso continúa hasta que el modelo converja.

El gradiente o la derivada de primer orden de la función de pérdida puede expresarse de la siguiente manera:

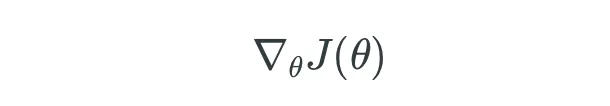
Luego, este gradiente se utiliza para actualizar el valor de las iteraciones anteriores del parámetro objetivo. Es decir:

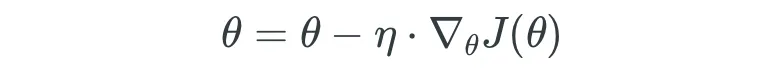
donde

• θ: Esto representa el/los parámetro(s) o peso(s) de un modelo que estás intentando optimizar. En muchos contextos, especialmente en redes neuronales, θ puede ser un vector que contiene muchos pesos individuales.
• η: Esta es la tasa de aprendizaje. Es un hiperparámetro que dicta el tamaño del paso en cada iteración al moverse hacia un mínimo de la función de costo. Una tasa de aprendizaje más pequeña puede hacer que la optimización sea más precisa, pero también podría ralentizar el proceso de convergencia, mientras que una tasa de aprendizaje más grande podría acelerar la convergencia, pero corre el riesgo de sobrepasar el mínimo. Puede ser [0,1], pero generalmente es un número entre (0.001 y 0.04).
• ∇J(θ): Este es el gradiente de la función de costo J respecto al parámetro θ. Indica la dirección y magnitud del aumento más pronunciado de J. Al restar esto del valor actual del parámetro (multiplicado por la tasa de aprendizaje), ajustamos θ en la dirección del decrecimiento más pronunciado de J.

Existen dos grandes desventajas en GD que hacen que esta técnica de optimización no sea tan popular, especialmente cuando se trata de conjuntos de datos grandes y complejos. Dado que en cada iteración, se debe utilizar y almacenar todos los datos de entrenamiento, el tiempo de cálculo puede ser muy largo y el proceso extremadamente lento. Además, almacenar esa gran cantidad de datos resulta en problemas de memoria, lo que hace que GD sea computacionalmente pesado y lento.

5.3 Descenso de Gradiente Estocástico (SGD)

El método Descenso de Gradiente Estocástico (SGD), también conocido como Descenso de Gradiente Incremental, es un enfoque iterativo para resolver problemas de optimización con una función objetivo diferenciable, al igual que GD.

Pero a diferencia de GD, SGD no utiliza el lote completo de datos de entrenamiento para actualizar el valor del parámetro en cada iteración. El método SGD a menudo se refiere como la aproximación estocástica del descenso de gradiente, que tiene como objetivo encontrar los puntos extremos o cero de un modelo estocástico que contiene parámetros que no se pueden estimar directamente.

SGD minimiza esta función de costo recorriendo los datos en el conjunto de datos de entrenamiento y actualizando los valores de los parámetros en cada iteración.

En SGD, todos los parámetros del modelo mejoran en cada paso de la iteración con solo una muestra de entrenamiento. Entonces, en lugar de recorrer todas las muestras de entrenamiento a la vez para modificar los parámetros del modelo, el algoritmo SGD mejora los parámetros observando un conjunto de entrenamiento único y aleatoriamente seleccionado (de ahí el nombre Estocástico). Esto es:

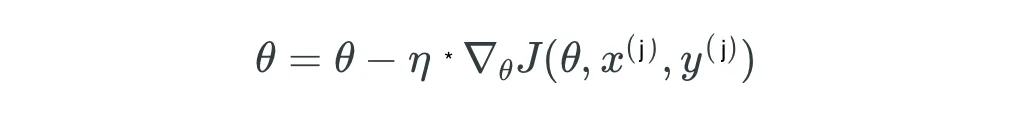
donde

• θ: Esto representa el parámetro o los pesos de un modelo que estás tratando de optimizar. En muchos contextos, especialmente en redes neuronales, θ puede ser un vector que contiene muchos pesos individuales.
• η: Esta es la tasa de aprendizaje. Es un hiperparámetro que dicta el tamaño del paso en cada iteración mientras se mueve hacia un mínimo de la función de costo. Una tasa de aprendizaje más pequeña puede hacer que la optimización sea más precisa, pero también puede ralentizar el proceso de convergencia, mientras que una tasa de aprendizaje más grande puede acelerar la convergencia, pero corre el riesgo de sobrepasar el mínimo.
• ∇J(θ,x(i),y(i)): Este es el gradiente de la función de costo J con respecto al parámetro θ para una entrada dada x(i) y su salida objetivo correspondiente y(i). Indica la dirección y magnitud del aumento más pronunciado de J. Al restar esto del valor actual del parámetro (multiplicado por la tasa de aprendizaje), ajustamos θ en la dirección de la disminución más pronunciada de J.
• x(i): Esto representa la muestra de datos de entrada número i de tu conjunto de datos.
• y(i): Esta es la salida objetivo real para la muestra de datos de entrada número i.

En el contexto del Descenso de Gradiente Estocástico (SGD), la regla de actualización se aplica a muestras de datos individuales x(i) y y(i) en lugar de todo el conjunto de datos, como sería el caso para el Descenso de Gradiente en lotes.

Este paso único mejora la velocidad del proceso de encontrar el mínimo global del problema de optimización y es lo que diferencia a SGD de GD. Por lo tanto, SGD ajusta constantemente los parámetros en un intento de moverse en dirección al mínimo global de la función objetivo.

SGD aborda el problema de tiempo de cálculo lento en GD, ya que es escalable tanto con grandes conjuntos de datos como con el tamaño del modelo. Sin embargo, aunque el método SGD en sí mismo es simple y rápido, se le considera un “mal optimizador” porque tiende a encontrar un óptimo local en lugar de un óptimo global.

En SGD, todos los parámetros del modelo se mejoran en cada paso de la iteración con solo una muestra de entrenamiento. Entonces, en lugar de recorrer todas las muestras de entrenamiento a la vez para modificar los parámetros del modelo, SGD mejora los parámetros observando una muestra de entrenamiento única.

Este paso único mejora la velocidad del proceso de encontrar el mínimo global del problema de optimización. Esto es lo que diferencia a SGD de GD.

5.4 SGD con momento

Cuando la función de error es compleja y no convexa, en lugar de encontrar el óptimo global, el algoritmo SGD se mueve por error en la dirección de diversos mínimos locales. Esto resulta en un mayor tiempo de cálculo.

Para abordar este problema y mejorar aún más el algoritmo SGD, se han introducido varios métodos. Una forma popular de escapar de un mínimo local y moverse en dirección a un mínimo global es SGD con Momento.

El objetivo del método SGD con momento es acelerar los vectores de gradiente en dirección al mínimo global, lo que resulta en una convergencia más rápida.

La idea detrás del momento es que los parámetros del modelo se aprenden utilizando las direcciones y los valores de ajuste de parámetros anteriores. Además, los valores de ajuste se calculan de tal manera que los ajustes más recientes tienen un peso mayor (obtienen pesos más grandes) en comparación con los ajustes tempranos (obtienen pesos más pequeños).

La razón de esta diferencia es que con el método SGD no determinamos la derivada exacta de la función de pérdida, sino que la estimamos en un pequeño lote. Dado que el gradiente es ruidoso, es probable que no siempre se mueva en la dirección óptima.

El momento ayuda a estimar esas derivadas de manera más precisa, lo que resulta en mejores elecciones de dirección al moverse hacia el mínimo global.

Otra razón de la diferencia en el rendimiento de SGD clásico y SGD con momento radica en el área llamada Curvatura Patológica, también llamada área de barranco.

La Curvatura Patológica o Área de Barranco se puede representar en el siguiente gráfico. La línea naranja representa el camino tomado por el método basado en el gradiente, mientras que la línea azul oscuro representa el camino ideal hacia la dirección de alcanzar el óptimo global.

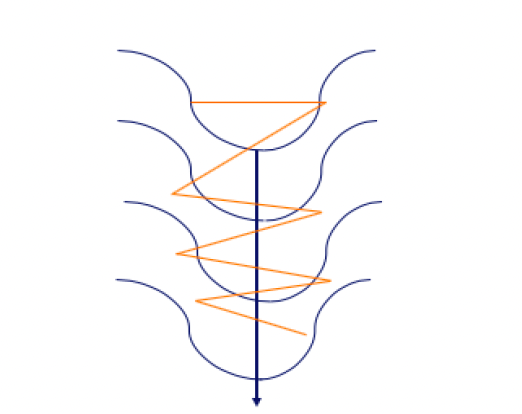
Para visualizar la diferencia entre SGD y SGD con Momento, echemos un vistazo a la siguiente figura.

En el lado izquierdo se encuentra el método SGD sin Momento. En el lado derecho se encuentra el SGD con Momento. El patrón naranja representa el camino del gradiente en busca del mínimo global.

La idea detrás del momento es que los parámetros del modelo se aprenden utilizando las direcciones y los valores de ajuste de parámetros anteriores. Además, los valores de ajuste se calculan de tal manera que los ajustes más recientes tienen un peso mayor (obtienen pesos más grandes) en comparación con los ajustes tempranos (obtienen pesos más pequeños).

5.5 Optimizador Adam

Otra técnica popular para mejorar el procedimiento de optimización SGD es la Estimación de Momento Adaptativo (Adam) introducida por Kingma and Ba (2015). Adam es la versión extendida del método SGD con momento.

La diferencia principal en comparación con SGD con momento, que utiliza una única tasa de aprendizaje para todas las actualizaciones de parámetros, es que el algoritmo Adam define diferentes tasas de aprendizaje para diferentes parámetros.

El algoritmo calcula las tasas de aprendizaje adaptativas individuales para cada parámetro en función de las estimaciones de los primeros dos momentos de los gradientes (primera y segunda derivada de la función de pérdida).

Por lo tanto, cada parámetro tiene una tasa de aprendizaje única, que se actualiza utilizando el promedio de decaimiento exponencial de los primeros momentos (la media) y los segundos momentos (la varianza) de los gradientes.

Puntos clave y qué viene a continuación

En este manual, hemos cubierto lo esencial y más en el aprendizaje automático. Desde los conceptos básicos hasta las técnicas avanzadas, hemos desglosado los algoritmos populares de aprendizaje automático utilizados globalmente en tecnología y los principales métodos de optimización que los impulsan.

Mientras aprendíamos sobre cada concepto, vimos algunos ejemplos prácticos y código de Python, asegurándonos de que no solo comprendes la teoría sino también su aplicación.

Tu viaje en el aprendizaje automático continúa y esta guía es tu referencia. No es una lectura única, sino un recurso para revisar a medida que progresas y prosperas en este campo. Con este conocimiento, estás listo para enfrentar la mayoría de los desafíos del aprendizaje automático del mundo real con confianza y a un nivel alto. Pero esto es solo el comienzo.

Sobre el Autor – ¡Ese Soy Yo!

Soy Tatev, Investigadora Senior de Machine Learning e Inteligencia Artificial. He tenido el privilegio de trabajar en Ciencia de Datos en numerosos países, incluyendo Estados Unidos, Reino Unido, Canadá y los Países Bajos.

Con un MSc y un BSc en Econometría en mi haber, mi trayectoria en Machine Learning e IA ha sido simplemente increíble. Basándome en mis estudios técnicos durante mi licenciatura y maestría, junto con más de 5 años de experiencia práctica en la industria de Ciencia de Datos, en Machine Learning e IA, he recopilado este resumen de alto nivel de temas de ML para compartir con ustedes.

¿Cómo puedes profundizar aún más?

Después de estudiar esta guía, si estás interesado en profundizar aún más y si el aprendizaje estructurado es tu estilo, considera unirte a nosotros en LunarTech. Sigue el curso “Fundamentos de Machine Learning“, un programa integral que ofrece una comprensión profunda de la teoría, implementación práctica práctica, material de práctica extenso y preparación de entrevistas personalizada para prepararte para el éxito en tu propia fase.

Este curso también forma parte de The Ultimate Data Science Bootcamp, que ha obtenido el reconocimiento de ser uno de los mejores bootcamps de Ciencia de Datos de 2023, y ha sido presentado en publicaciones de renombre como Forbes, Yahoo, Entrepreneur y más. Esta es tu oportunidad de ser parte de una comunidad que prospera en la innovación y el conocimiento. Puedes inscribirte en una prueba gratuita de The Ultimate Data Science Bootcamp en LunarTech.

No solo para gigantes tecnológicos: así es como LunarTech revoluciona el aprendizaje de ciencia de datos e IA. En la era digital, donde el mundo está en constante cambio, Tatev Aslanyan y Vahe Aslanyan se han unido para redefinir la educación en IA. En un aula digital vibrante, una cohorte diversa de estudiantes, muchos provenientes de diversos antecedentes no técnicos, se sumergen en el mundo de la ciencia de datos. No están simplemente absorbiendo…AJ Ignacio – Colaborador de la Marca Forbes Australia

Superando a la competencia: cómo LunarTech está redefiniendo el futuro de la IA y el Machine Learning | EntrepreneurAnne SchulzeEntrepreneur Georgia

LunarTech lanza un bootcamp de educación en ciencia de datos que cambia el juego, haciendo que la IA y el Machine Learning avanzado sean accesibles para todosAustin, Texas – (Newsfile Corp. – 25 de agosto de 2023) – LunarTech, una innovadora plataforma de educación tecnológica en línea, se complace en anunciar el lanzamiento de su…Newsfile Corp.Yahoo Finance

Conéctate conmigo:

• Sígueme en LinkedIn para obtener un montón de recursos gratuitos en ML y AI
• Visita mi sitio web personal
• Suscríbete a mi El Boletín de Ciencia de Datos y AI

El Boletín de Ciencia de Datos y AI | Tatev Karen | SubstackDel creador del Bootcamp de Ciencia de Datos mejor valorado de 2023, confiado por más de 1 millón de lectores de blogs: ¡Descubre nuestro exclusivo boletín! Obtén lo último en Ciencia de Datos y AI, como se ve en Forbes, Entrepreneur. Mejora tu experiencia. ¡Suscríbete y sé innovador en tecnología!Tatev KarenEl Boletín de Ciencia de Datos y AI

¿Quieres descubrir todo sobre una carrera en Ciencia de Datos, Aprendizaje Automático e IA, y aprender cómo conseguir un trabajo en Ciencia de Datos? Descarga este Manual de Carrera en Ciencia de Datos y AI GRATIS

Gracias por elegir esta guía como tu compañero de aprendizaje. A medida que sigas explorando el vasto campo del aprendizaje automático, espero que lo hagas con confianza, precisión y espíritu innovador. ¡Mis mejores deseos en todos tus futuros proyectos!

---

• Artificial Intelligence
• Data Science
• Machine Learning
• Python